Il nuovo calcestruzzo – Temperatura e calcestruzzo
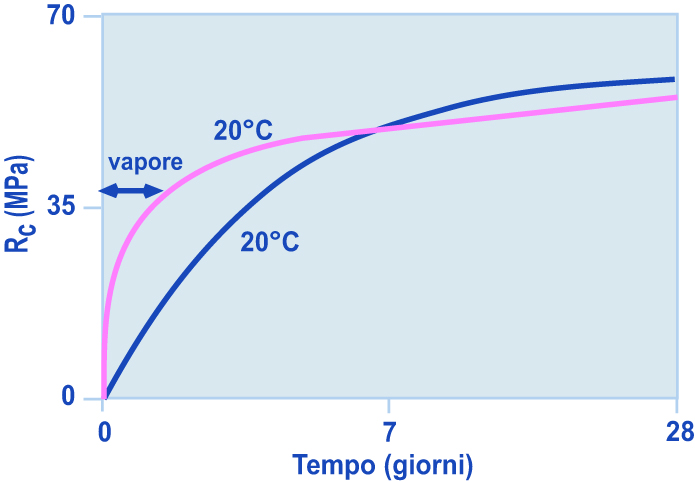
Fig. 14.4 – Influenza del trattamento a vapore sulla resistenza meccanica a compressione (Rc) rispetto a quella dello stesso calcestruzzo stagionato sempre a 20°C
14.5 CALORE DI IDRATAZIONE, GRADIENTI TERMICI E RISCHI DI FESSURAZIONE
L’idratazione del cemento è una reazione esotermica che avviene con sviluppo di calore. Il calore di idratazione unitario, cioè riferito ad 1 kg di cemento, dipende dal tipo e dalla classe di resistenza del cemento: maggiori sono il contenuto di clinker Portland e la finezza di cemento (cioè la classe di resistenza), più rapido è lo sviluppo di calore (Tabella 14.2).
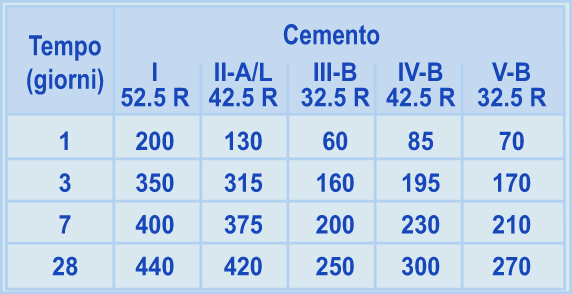
Tabella 14.2 – Calore di idratazione (kJ/kg) di alcuni cementi a vari tempi di idratazione
Il calore di idratazione provoca il riscaldamento del calcestruzzo. In condizioni adiabatiche, cioè in assenza di alcuna perdita di calore dal calcestruzzo, l’aumento di temperatura (ΔTt )ad , al tempo t, può essere così calcolato: 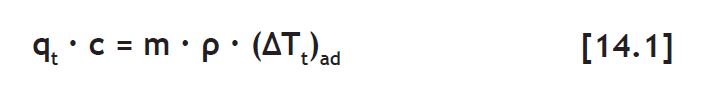
dove qt (in kJ/kg) è il calore di idratazione unitario del cemento al tempo t (Tabella 14.2), c è il dosaggio di cemento nel calcestruzzo (in kg/m3), qt · c (in kJ/m3 di calcestruzzo) è il calore sviluppato in 1 m3 di calcestruzzo al tempo t, m è la massa di 1 m3 di calcestruzzo (≈2400 kg/m3), ρ è il calore specifi co del calcestruzzo [≈1,1 kJ/(kg·°C)]. In Fig. 14.5 è riportato il riscaldamento (ΔTt )ad in funzione del tempo di idratazione (t) per un calcestruzzo con cemento CEM II/A-L 42.5R (300 kg/m3) in condizioni adiabatiche:
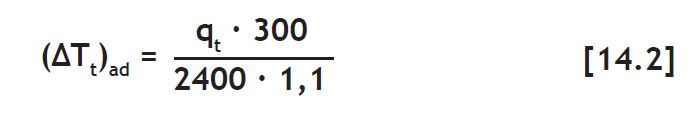
Inserendo nella [14.2] il valore di q<sub>t</sub> ai vari tempi (Tabella 14.2) si ricava la curva di Fig. 14.5.
Nel caso di un riscaldamento non adiabatico, come si verifica usualmente nelle strutture reali, l’andamento della temperatura sarà prima crescente (quando nei primi 2-3 giorni il calore d’idratazione si sviluppa ad alta velocità), e dopo decrescente (quando la dissipazione del calore dal calcestruzzo all’ambiente prevale sullo sviluppo del calore di idratazione che dopo 3 giorni procede più lentamente). Nella Fig. 14.6 è mostrato esemplificativamente ΔT<sub>t</sub> (in condizioni non adiabatiche) in funzione del tempo (t) in una zona della struttura termicamente più isolata (nucleo) ed in una zona corticale periferica dove il calore di idratazione è dissipato più rapidamente.
A causa del diverso isolamento termico del calcestruzzo nella zona centrale (nucleo) ed in quella periferica, si instaura un gradiente termico (δTt) tra la parte più calda e quella più fredda della struttura*. Il massimo valore del gradiente termico (δT)max si raggiunge solitamente a 2-3 giorni e comunque raramente oltre 7 giorni.
* ΔTt, rappresenta la variazione di temperatura (riscaldamento) in funzione del tempo (t) nello stesso punto della struttura; δ Tt rappresenta la differenza di temperatura (gradiente termico), ad un determinato tempo (t), tra due diversi punti della struttura (nel caso specifico tra il nucleo, più caldo, e la periferia, più fredda)
Se il valore di (δT)max supera 20°C esiste un rischio di fessurazione per le tensioni conseguenti alle differenti variazioni dimensionali (Fig. 14.6). La fessurazione potrà apparire sulla superficie durante i primi 2-3 giorni (cioè nella fase di riscaldamento in Fig. 14.7) a causa delle tensioni di compressione nel nucleo più caldo (che vorrebbe dilatarsi) che provoca tensioni di trazione sulla superficie più fredda della struttura che si dilata meno del nucleo; in realtà questo tipo di rischio, che pure esiste, non è elevatissimo (se non in calcestruzzi molto ricchi di cemento ed in climi freddi) perché inizialmente il modulo elastico (§ 9.7) è basso e, quindi, si instaurano basse tensioni a causa delle differenze termiche. Inoltre, si registra un rilassamento viscoso che mitiga le tensioni insorte tra nucleo e periferia (§ 16.1).

Fig. 14.5 – Incremento di temperatura, (ΔTt)ad, cioè il riscaldamento in funzione del tempo (t) nel nucleo di un calcestruzzo in condizioni adiabatiche: 300 kg/m3 di CEM II/A-L 42.5R

Fig. 14.6 – Esempio di fessure indotte da un eccessivo gradiente termico (40°C) tra nucleo più caldo e spigoli di un pilastro più freddi
La fessurazione potrà verificarsi nel nucleo della struttura (quindi più insidiosamente perché non visibile) nella fase di raffreddamento di Fig. 14.7 per l’insorgere di tensioni di trazione nel nucleo che si raffredda più lentamente della periferia. Poiché nel frattempo il calcestruzzo è diventato più rigido, cioè è aumentato il modulo elastico, le variazioni dimensionali di origine termica provocano una maggiore tensione. Inoltre, il rilassamento viscoso va diminuendo con l’aumento di rigidità del sistema, e quindi gioca un ruolo meno importante nel mitigare le tensioni.
Mentre il calcolo di (ΔTt )ad in condizioni adiabatiche attraverso la [14.2] è relativamente semplice, il calcolo di (δT)t è troppo complesso poiché dipende anche da fattori difficilmente prevedibili (condizioni eoliche e termiche nei giorni immediatamente dopo il getto) che influenzano la dispersione del calore, oltre che dalle dimensioni e dalla geometria delle strutture. Tuttavia, è possibile calcolare il valore di (δT)max nella ipotesi estrema e conservativa di riscaldamento adiabatico nel nucleo e di dissipazione termica totale in periferia (temperatura sempre eguale a quella dell’ambiente): in queste condizioni il valore di (δTt)max coincide con quello di (ΔTt)ad , cioè la differenza di temperatura tra nucleo e periferia (Fig. 14.7) coincide con il riscaldamento adiabatico del nucleo (Fig. 14.5).

Fig. 14.7 – Variazioni della temperatura (ΔTt) nel nucleo e nella periferia, in funzione del tempo (t) con formazione di gradienti termici (δTt) in calcestruzzo in condizioni non adiabatiche: 300 kg/m3 di CEM II/A-L 42.5R
Assumendo realisticamente che il (δTt)max è raggiunto solitamente a tre giorni si può porre:

Attraverso la [14.1] si ottiene
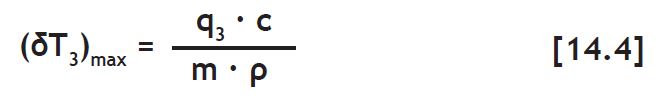
dove q3 è il calore di idratazione sviluppato da 1 kg di cemento a 3 giorni (Ta-bella 14.2); c è il dosaggio di cemento in kg/m3, m è la massa volumica del calcestruzzo (circa 2400 kg/m3) e ρ è il calore specifico del calcestruzzo, circa 1,1 kJ/ (Kg∙°C).
Se si pone (δTt)max eguale a 20°C (massimo gradiente termico accettabile, oltre il quale esiste il rischio di fessurazione) si ottiene:

Inserendo 2400 kg/m3 al posto di m, e 1,1 kJ/(kg·°C) al posto di ρ si ottiene:

Scegliendo il tipo di cemento e conseguentemente il valore di q3 dalla Tabella 14.2, si può calcolare il massimo dosaggio di cemento (c), attraverso la [14.6], per non superare il gradiente termico (δT3)max di 20°C. Per esempio il valore del dosaggio di cemento (c) diventa 168 kg/m3 con il CEM II A-L 42.5R e 330 kg/ m3 se si sceglie il CEM III/B 42.5N per effetto di un minor calore di idratazione (q3=315 e 160 kJ/kg rispettivamente per il cemento al calcare ed il cemento d’altoforno).
Bibliografia consigliata:
- Lorella Angelini, Vincenzo Maniscalco, Mario Collepardi; “Calcestruzzo stagionato
a vapore a bassa temperatura (20-40°C)”; Atti delle Giornate AICAP
1985; 2-4 Maggio; 1985 - Mario Collepardi; “Scienza e Tecnologia del Calcestruzzo”; Terza Edizione;
Hoepli; Milano; 1991 - Mario Collepardi, Silvia Collepardi e Roberto Troli; “Il Mix Design del Calcestruzzo”;
Editore Tintoretto, Villorba (TV); 2008 - Vito Alunno Rossetti; “Il Calcestruzzo. Materiali e Tecnologia”; Mc Graw Hill
Italia Milano; 1997
