A B C Calcestruzzo Archives - Pagina 2 di 3

Mix-design del calcestruzzo

Mix-design è letteralmente il “progetto della miscela“; più estesamente è il “calcolo della composizione del calcestruzzo a partire dalle prestazioni richieste (lavorabilità, resistenza meccanica, durabilità, ecc.) e dalle caratteristiche delle materie prime disponibili (cemento, inerti, additivi)“. Secondo una corretta accezione del termine, il mix-design si basa su alcune correlazioni sperimentali esistenti tra la composizione del calcestruzzo, da una parte, e le prestazioni del calcestruzzo e le caratteristiche delle materie dall’altra. Le cinque correlazioni fondamentali, illustrate in Fig. 1, sono:1 – il quantitativo di acqua (a), in kg/m³, dipende dalla lavorabilità del conglomerato fresco, oltre che dal tipo di inerte (tondeggiante o frantumato), dalla sua dimensione (diametro massimo), e dalla presenza di additivi (riduttori di acqua e aeranti);2 – il rapporto tra il quantitativo di acqua e quello di cemento che occorre adottare – rapporto a/c – dipende dalla resistenza meccanica del conglomerato indurito (R_ck), oltre che dal tipo e dalla classe del cemento;3 – il rapporto a/c che occorre adottare dipende anche dalla durabilità del conglomerato indurito in relazione al grado di aggressione ambientale (classe di esposizione) cui la struttura è esposta;4 – noto il valore di a (attraverso la correlazione 1) e calcolato il valore di c (attraverso il valore di a e quello di a/c, quest’ultimo in base alle correlazioni 2 e 3) si calcola il volume di inerte V_i per differenza attraverso un bilancio di volume sottraendo al volume del calcestruzzo V_cls, quelli degli altri ingredienti V_a, V_c e V_a‘, (rispettivamente i volumi di acqua, cemento ed aria: i primi due sono calcolati dalle masse a e c attraverso le corrispondenti masse volumiche, il terzo V_a‘ è ricavato sperimentalmente in base al diametro massimo dell’inerte (D_max);5 – il volume V_i dell’inerte totale viene ripartito in quello dei singoli inerti (per esempio sabbia e ghiaia) in base alle curve granulometriche di questi ultimi rispetto alla curva ottimale prescelta (Fuller, Bolomey, ecc.). I volumi di sabbia (V_s) e di ghiaia (V_g) così ottenuti vengono convertiti nelle corrispondenti masse (s e g) moltiplicando i volumi per le corrispondenti masse volumiche m_s ed m_g.Nei paragrafi che seguono vengono illustrate le cinque correlazioni soprammenzionate.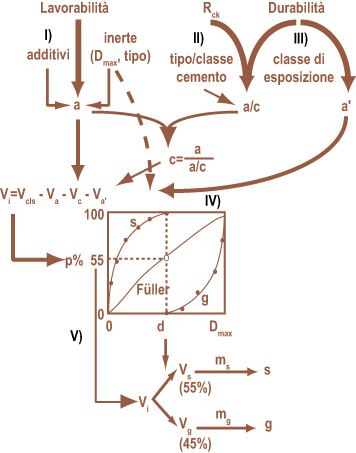 Fig. 1 – Schematizzazione del processo di mix-design attraverso cinque correlazioni

LAVORABILITÀ, ACQUA, INERTE, ADDITIVI

La correlazione I è illustrata nella Fig. 2 e mostra come all’aumentare della lavorabilità richiesta (in termini di slump) occorre proporzionalmente aumentare il quantitativo di acqua di impasto (a). Tuttavia esistono diverse curve di correlazione tra slump ed a, a seconda del diametro massimo. In altre parole, fissato lo slump richiesto (per esempio 180 mm), la quantità di acqua a, che occorre impiegare per conseguire questa lavorabilità, è tanto minore quanto più grosso è l’inerte: infatti, aumentando il diametro massimo (D_max), si riduce l’area superficiale specifica dell’inerte e quindi l’acqua necessaria per bagnare la superficie; per esempio, per ottenere un calcestruzzo con uno slump di 180 mm, occorrono 240 kg/m³ oppure 210 kg/m³ di acqua a seconda che il diametro massimo dell’inerte è 16 oppure 32 mm rispettivamente (Fig. 2).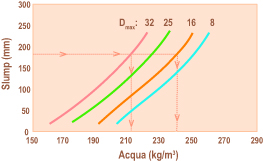Fig. 2 – Influenza del diametro massimo (D_max) dell’inerte sulla correlazione slump-acqua di impasto.In realtà, a parità di D_max, la quantità d’acqua che occorre impiegare per confezionare un calcestruzzo con un determinato slump, è maggiore se si utilizza un inerte frantumato dal contorno irregolare piuttosto che un inerte alluvionale dal contorno tondeggiante: infatti, a parità di dimensione, un inerte dal contorno irregolare, rispetto a quello dal contorno tondeggiante, presenta un attrito maggiore nei confronti della matrice cementizia e richiede, quindi, un maggior quantitativo di acqua per conseguire la stessa lavorabilità, cioè la stessa mobilità, del calcestruzzo fresco. Pertanto, i valori medi di acqua di impasto riportati in Fig. 2 debbono essere aumentati di 10 kg/m³ se si tratta di inerti frantumati dal contorno irregolare, e diminuiti di 10 kg/m³ se si tratta di inerti alluvionali dal contorno tondeggiante.La Fig.2 mostra, come si è visto, la variazione dello slump con il quantitativo di acqua di impasto (a) per un determinato inerte (tipo e diametro massimo).Se, però, si impiegano alcuni additivi, si riduce il quantitativo di acqua richiesto per ottenere un determinato slump con un certo inerte. La riduzione di acqua di impasto è funzione del tipo e dosaggio di additivo. Queste sono alcune tipiche riduzioni espresse in percentuale rispetto ai quantitativi di acqua mostrati in Fig. 2:5% se si impiega un additivo aerante (0.04-0.06% sul cemento), in caso di esposizione del calcestruzzo ai cicli di gelo-disgelo;8% se si impiega un additivo fluidificante (0.3-0.4% sul cemento);20% se si impiega un additivo superfluidificante (0.8-1.2% sul cemento);30% se si impiega un additivo iperfluidificante (1.5-2% sul cemento).Per esempio, per confezionare un calcestruzzo con slump di 180 mm il valore di a, in assenza di additivi, è di 200 kg/m³ con un inerte tondeggiante di 32 mm: in presenza di additivo superfluidificante, il valore di a per questo calcestruzzo si riduce del 20% è diventa 160 kg/m³.

RESISTENZA CARATTERISTICA, CEMENTO E RAPPORTO A/C

La correlazione 2 è illustrata nella Fig. 3 che mostra come la resistenza caratteristica R_ck (controllo di tipo A, R_ck = R_cm28-3.5), dove R_cm28 è la resistenza media a 28 giorni in MPa) aumenta al diminuire del rapporto a/c.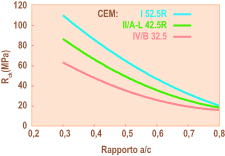Fig. 3 – Correlazione della R_ck con il rapporto a/c per tre diversi cementi.In realtà la correlazione R_ck – a/c (ricavata sperimentalmente misurando la resistenza meccanica media di calcestruzzi con rapporto a/c noto) dipende anche dal tipo e soprattutto dalla classe del cemento impiegato. Nella Fig. 3 sono mostrate, a titolo di esempio, le curve di correlazione R_ck – a/c per tre cementi CEM I 52.5R, CEM II A/L 42.5R, CEM IV/B 32.5. In realtà è possibile tracciare una curva per ognuno dei 150 cementi previsti dalla norma UNI – EN 197/1. Tuttavia, tenendo conto delle effettive prestazioni dei vari cementi è possibile raggruppare in pratica tutte le potenziali correlazioni R_ck – a/c in tre gruppi; a seconda della classe di resistenza ed indipendentemente dal tipo: una prima per i cementi di classe 52.5 e 52.5R; una seconda per i cementi di classe 42.5 e 42.5R; una terza per i cementi di classe 32.5 e 32.5R.Se, invece, anziché la R_ck – che si riferisce a 28 giorni – è presa in considerazione una resistenza meccanica alle brevi stagionature, per esempio per motivi di scasseratura a 1 giorno, allora occorre disporre di altre correlazioni, simili a quelle mostrate in Fig. 3, ma riferite a tempi di stagionatura più brevi.

DURABILITÀ, RAPPORTO A/C ED ARIA INGLOBATA

L’assetto normativo, quale emerge dalle nuove regole europee sulla produzione e messa in opera del calcestruzzo, annette un’importanza fondamentale al problema della durabilità: l’impianto logico è incentrato su questi tre punti essenziali che interferiscono pesantemente con il processo di mix-design:1 – classificare gli ambienti in base al loro carattere aggressivo nei confronti del calcestruzzo e/o dei ferri di armatura (classi di esposizione);2 – adottare, conseguentemente, un rapporto a/c tanto più basso quanto maggiore è il livello di aggressione ambientale per predisporre un calcestruzzo impermeabile alla penetrazione degli agenti aggressivi;3 – inglobare aria in forma di microbolle uniformemente distribuite nella matrice cementizia (ed in misura tanto maggiore quanto minore è il diametro massimo dell’inerte) nei calcestruzzi esposti ai cicli di gelo-disgelo.Un altro aspetto fondamentale per la durabilità delle strutture – che non è in relazione con il mix-design, ma piuttosto con il processo esecutivo – è garantire un periodo minimo di stagionatura umida o di protezione dall’evaporazione (3 – 7 giorni) – che deve essere tanto più lungo, quanto più asciutto e freddo è il clima al momento della scasseratura.Tornando ai suddetti tre punti fondamentali per l’interazione della durabilità con la composizione del calcestruzzo, per ragioni di semplicità e brevità espositiva si farà riferimento all’attuale normativa (EN 206). Nella Tabella 1 sono mostrati i valori massimi di a/c e minimi di a‘ (aria, % in volume) in relazione alla classe di esposizione ambientale ed alla tipologia strutturale (normale, armata, precompressa), così come appaiono nella vigente norma europea e nazionale; per ragioni di comodità, sono anche riportati i valori minimi del copriferro per le strutture in c.a. e c.a.p. come previsti dall’Eurocodice 2.Selezionata la classe di esposizione ambientale nella quale l’opera è destinata a sorgere (per esempio 2a), e scelta la tipologia strutturale (per esempio armata), si individua il valore di (a/c)’ – in questo caso 0.60 – che non deve essere superato nel confezionare l’impasto se non si vuole mettere a rischio la durabilità dell’opera. Questo valore va confrontato con il rapporto a/c correlato con la R_ck (scelta per ragioni di calcolo strutturale) in base ai grafici di Fig.4. Sono possibili tre situazioni:A) il valore del rapporto acqua-cemento (a/c)’ imposto dai vincoli di durabilità (Tabella 1) coincide con quello (a/c) derivante dalla R_ck (Fig. 4): in questo caso non esistono, ovviamente, problemi sulla scelta di a/c e quindi per la prosecuzione del mix-design;B) il valore di (a/c)’ imposto dai vincoli di durabilità è maggiore di quello (a/c) derivante dalla R_ck; in questo caso, che si verifica solitamente per valori di R_ck elevati, si sceglie, per la prosecuzione del mix-design, il valore di a/c derivante dalla R_ck il quale soddisfa anche il vincolo nel rapporto (a/c)’ massimo imposto dalla durabilità;C) il valore di (a/c)’ imposto dalla durabilità è inferiore a quello di (a/c) derivante dalla R_ck; in questo caso, che si verifica quasi sempre per valori di R_ck bassi o medio-bassi (15-25 MPa), il valore del rapporto acqua-cemento con cui proseguire il mix-design è quello (a/c)’ imposto dalla durabilità, ed il valore di resistenza caratteristica risulterà di fatto più alto (R‘_ck) rispetto a quello previsto originariamente (R_ck) sulla base di considerazioni meramente strutturali.Quest’ultimo aspetto del problema, che è un punto chiave nel processo di mix-design in relazione alle due proprietà fondamentali del calcestruzzo in servizio (resistenza meccanica e durabilità) è illustrato esemplificativamente nella Fig. 4 dove è riportata la resistenza caratteristica in funzione del rapporto acqua-cemento per un determinato cemento (per esempio CEM II B/L 32.5R).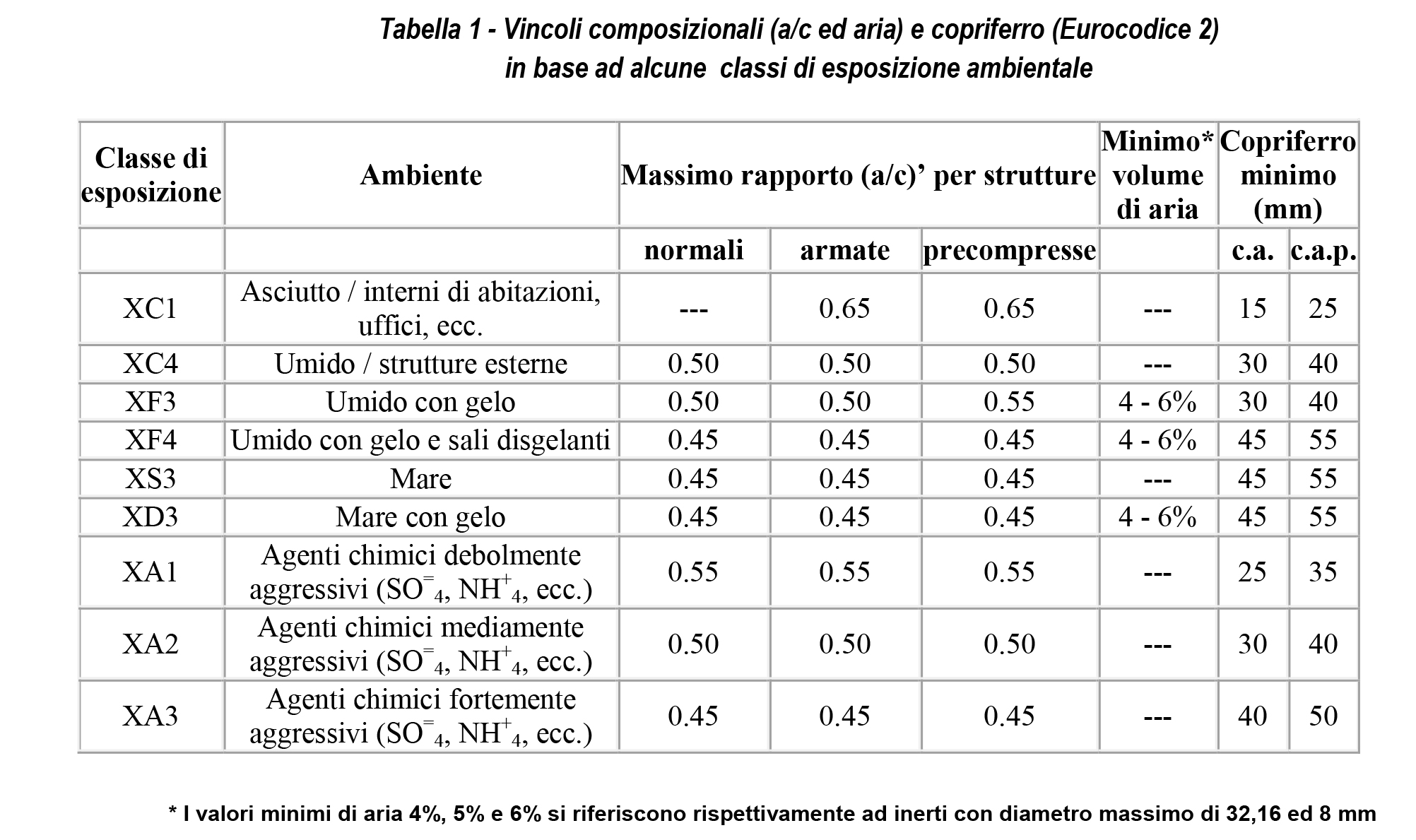Tabella 1 – Vincoli composizionali (a/c ed aria) e copriferro (Eurocodice 2) in base ad alcune classi di esposizione ambientaleScelto R_ck (per es. 25 MPa) si individua a/c (0.63); ma poiché questo è maggiore di (a/c)’ imposto dal vincolo di durabilità (per es. 0.50) occorre, tra i due valori del rapporto acqua/cemento, scegliere il più basso tra i due – cioè 0.50 – in modo da soddisfare sia il requisito di durabilità che quello di resistenza caratteristica. Naturalmente, la effettiva resistenza caratteristica sarà R‘_ck =36 MPa > R_ck= 25 MPa (inizialmente prevista solo per ragioni strutturali) in virtù del minor rapporto (a/c)’ che si deve adottare per ragioni di durabilità.* I valori minimi di aria 4%, 5% e 6% si riferiscono rispettivamente ad inerti con diametro massimo di 32,16 ed 8 mmNel caso delle classi di esposizione XF3, XF4 e XD3 ai fini della durabilità è previsto un volume minimo di aria (si consulti l’articolo “Gelo e disgelo nel calcestruzzo” sul sito www.encosrl.it è l’ABC del calcestruzzo).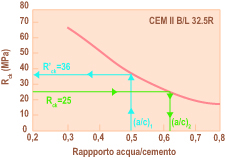Fig.4 – Scelta della effettiva resistenza caratteristica (R’ck) per ragioni di durabilità(Tabella 1), occorre prevedere l’impiego di un additivo aerante e modificare la correlazione resistenza meccanica – rapporto a/c (Fig. 5) per tener conto della presenza delle microbolle d’aria (4-6% in volume). Infatti, l’aria inglobata, benefica per la resistenza ai cicli di gelo-disgelo, comporta una penalizzazione della prestazione meccanica di circa il 20%. Ciò significa che – in presenza di additivo aerante – la curva della Fig. 4 risulta abbassata di un 20% sull’ordinata come è mostrato in Fig. 5. Conseguentemente, per un dato valore di R_ck, l’impiego di additivo aerante comporta un valore nel rapporto acqua-cemento (a/c)₂ più basso di quello (a/c)₁ che occorrerebbe impiegare in assenza di aerante (Fig. 5).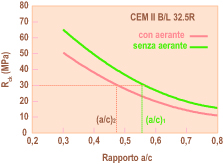Fig.5 – Correlazione tra resistenza caratteristica e rapporto acqua-cemento con e senza aerante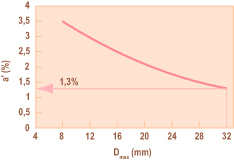Fig.6 – Volume di aria intrappolata (a’) nel calcestruzzo compattato in funzione del diametro massimo dell’inerte (con Dmax=32 mm), la percentuale di aria è 1.3%.

COMBINAZIONE DEGLI INERTI DISPONIBILI

Noti i valori di a (Fig. 2) e quello di a/c (Fig. 4), si passa al calcolo del volume totale di inerte (V_i) per bilancio di volume tra quello del calcestruzzo (V_cls), da una parte, e quelli dei singoli ingredienti, dall’altra:V_i = V_cls – V_a – V_c – V_a‘ [1]dove V_a e V_c, rispettivamente i volumi di acqua e di cemento, sono facilmente calcolabili dalle corrispondenti masse volumiche (1 kg/l per l’acqua e circa 3.1 kg/l per il cemento), mentre V_a‘ è il volume di aria in litri per volume unitario di calcestruzzo, pari a 10 volte la % di aria nel calcestruzzo. Ponendo V_cls pari a 1 m³ ed esprimendo tutti i volumi in litri la [1] diventa:V_i = 1000 – a – (c/3.1) – 10 a‘ [2]dove V_i è il volume di inerte totale in litri per 1 m³ di calcestruzzo, ed a‘ è la percentuale in volume di aria presente nel conglomerato. Nel caso di calcestruzzi resistenti al gelo il valore di a‘ (aria inglobata) è desunto dalla Tabella 1 per esigenza di durabilità; per tutte le altre classi di esposizione cioè per i calcestruzzi privi di aerante, il valore di a‘ (aria intrappolata) è deducibile dalla Fig. 6 che riporta la percentuale di aria, misurata sperimentalmente nel calcestruzzo dopo compattazione, in funzione del diametro massimo dell’inerte sceltoNoto a‘ (dalla Tabella 1 o dalla Fig. 6, a seconda delle classi di esposizione), è possibile risalire al volume dell’inerte totale (V_i) mediante l’equazione [2]. Per esempio con D_max di 32 mm, con a di 160 kg/m³ (slump = 180 mm, con inerte tondo e superfluidificante), con c di 320 kg/m³ in base ad a/c=0.50 ed a = 160 kg/m³, si può calcolare V_i se si assume che la percentuale di aria intrappolata (a‘) è di 1.3% (Fig.6):V_i = 1000 – 160 – ( 320/3.1) – 13= 724 l/m³Nel caso, per esempio, che gli inerti reali disponibili siano una sabbia ed una ghiaia con D_max = 32 mm, il valore di (V_i) di tutto l’inerte deve essere suddiviso nel volume di sabbia (V_s) e di ghiaia (V_g) per 1 m³ di calcestruzzo. Per questa operazione finale del mix-design, nota come combinazione degli inerti, è necessario disporre delle analisi granulometriche (determinate per vagliatura) della sabbia e della ghiaia, e della distribuzione granulometrica ottimale (secondo Fuller, Bolomey o altri) che si vuole conseguire. Questa operazione è descritta in dettaglio nell’articolo “Inerte del calcestruzzo” disponibile sul sito www.enco.srl è l’ ABC del calcestruzzo.Una volta calcolati V_s e V_g, entrambi espressi in litri per 1 m³ di calcestruzzo, è possibile risalire alle masse di sabbia (s) e di ghiaia (g), in kg per 1 m³ di calcestruzzo, moltiplicando V_s e V_g per le corrispondenti masse volumiche (pesi specifici), rispettivamente della sabbia (m_s) e della ghiaia (m_g). I valori delle masse volumiche della sabbia e della ghiaia sono solitamente compresi nell’intervallo (2.6 – 2.7 kg/l) e vanno determinati nella condizione di inerti saturi (di umidità) a superficie asciutta (s.s.a.), cioè nella condizione in cui essi si trovano all’interno dell’impasto.

PER CONCLUDERE

Il mix-design può essere approfondito per determinare anche il ritiro, la deformazione viscosa, il modulo elastico, la resistenza meccanica a flessione o a trazione, la resistenza meccanica allo scassero, il calore di idratazione, i gradienti termici – tutte proprietà ingegneristiche importanti, ma solitamente richieste per casi un po’ particolari. Così pure, sempre attraverso il mix-design si può entrare nel merito del trasporto del calcestruzzo e della corrispondente perdita di lavorabilità, dell’impiego di additivi riduttori di acqua o acceleranti, della correzione da apportare alla “ricetta” per tener conto dell’umidità degli inerti, o di altri dettagli esecutivi.

Non-distruttive: prove sul calcestruzzo in opera

La diagnosi del deterioramento di una struttura consiste nella raccolta di dati sperimentali che — unitamente alle informazioni al contorno, di carattere ambientale, climatico, storico, strutturale — consente di stabilire le cause del deterioramento della struttura in genere, e del degrado dei materiali in particolare. La raccolta di dati sperimentali si basa sull’esecuzione di prove che possono essere suddivise in distruttive e non-distruttive.La distinzione tra prove distruttive e non-distruttive consiste fondamentalmente nel fatto che le prime si basano su prove sperimentali, generalmente eseguite in laboratorio, effettuate su provini o campioni prelevati dalla struttura: ne consegue che esse prevedono in genere il sollevamento sia pure parziale di un pavimento, il carotaggio di una muratura, ecc., tutte operazioni che possono arrecare una compromissione alle strutture sospettate di essere coinvolte da un processo di deterioramento.Le prove non-distruttive, invece, presentano il vantaggio di fornire elementi utili alla interpretazione del potenziale deterioramento in atto, senza minimamente aggravare lo stato della struttura dal punto di vista estetico o strutturale. Le prove non-distruttive sono di carattere prevalentemente fisico o fisico-meccanico da eseguire in sito sulla struttura; le prove distruttive, invece, sono di carattere chimico, fisico, o meccanico da effettuare in laboratorio.In generale, è molto difficile che con le sole prove non-distruttive si possa arrivare ad una diagnosi corretta del degrado di una struttura. Molto spesso, esse debbono essere accompagnate da quelle distruttive. L’accoppiamento di prove distruttive e non-distruttive, oltre al carattere di complementarità e di completezza dell’informazione desunta, presenta anche il vantaggio di ridurre globalmente il numero totale delle prove da eseguire e quindi il costo generale della diagnosi: infatti, in linea di massima, il costo della singola prova di laboratorio è relativamente basso, ma si richiede un numero relativamente elevato di prove sui diversi prelievi, rispetto alle prove non distruttive, per poter emettere una diagnosi.Lo scopo principale delle prove non-distruttive in sito è quello di fornire elementi utili non tanto e non solo per emettere direttamente una diagnosi, quanto e soprattutto per guidare il tecnico in un prelievo ben finalizzato dei campioni e dei provini da sottoporre a successive prove di laboratorio. Le prove non-distruttive sono in genere caratterizzate dalle seguenti proprietà:· mantengono integra (o quasi) la struttura indagata;

informano in modo globale, rapido e semplice;
forniscono risultati sia qualitativi che quantitativi o comunque comparativi.

Le principali prove non-distruttive che possono essere prese in considerazione per una diagnosi delle strutture includono: fotografia, termografia, endoscopia, magnetometria, gammagrafia, auscultazione sonica, prove con ultrasuoni e sclerometria.

FOTOGRAFIA

Per quanto banale essa possa sembrare, la documentazione fotografica (Fig. 1) è una prova non-distruttiva che sempre dovrebbe accompagnare una diagnosi, anche e soprattutto se seguita da prove distruttive in laboratorio, per evidenziare e documentare dove sono localizzati i prelievi sottoposti alle altre osservazioni o analisi. Essa dovrebbe includere sia la visione d’assieme della struttura da indagare, sia i dettagli possibilmente identificati con un codice per consentire un facile ed immediato riferimento alla struttura generale.

TERMOGRAFIA

Il principio della termografia è basato sul fatto che qualsiasi oggetto che si trova ad una determinata temperatura emette un flusso di energia regolato dalla legge dì Stefan-Bolzmann:E= esT⁴dove T è la temperatura assoluta (in °K) della superficie da cui proviene il flusso energetico E (in W/m²), s è una costante che vale 5,67 · 10^-8 W/m²°K⁴, ed e una costante adimensionale — detta emissività — che dipende dal materiale che costituisce la superficie.

Fig. 1 – Esempio di documentazione fotografica per la diagnosi del degrado.

Immaginando che una struttura composita, come una muratura, sia esposta nelle stesse condizioni termiche (per esempio all’irraggiamento solare), i singoli elementi (pietra, malta, mattone, acciaio, ecc.) si porteranno ad una diversa temperatura in funzione delle loro proprietà termiche, ed in particolare del loro calore specifico e della loro conducibilità termica. Ciascun elemento emetterà un flusso di energia in accordo con la legge di Stefan-Bolzmann, in funzione della temperatura raggiunta e della sua emissività. La termografia consiste nel registrare, mediante un rilevatore ad infrarosso, le temperature raggiunte dai vari elementi presenti in una struttura. Il rilevatore impiegato consente, in particolare, di misurare le radiazioni infrarosse (IR) comprese nell’intervallo di lunghezza d’onda tra 2 e circa 6 mm. Mediante un sistema ottico (costituito da varie lenti) ed elettrico (capace di tramutare in un segnale elettrico l’intensità della radiazione ricevuta) le differenze di temperature vengono registrate, attraverso un termogramma consistente nella registrazione grafica di tonalità monocromatiche (varianti, per esempio, dal bianco al nero) proporzionali alle diverse temperature (Fig. 2).

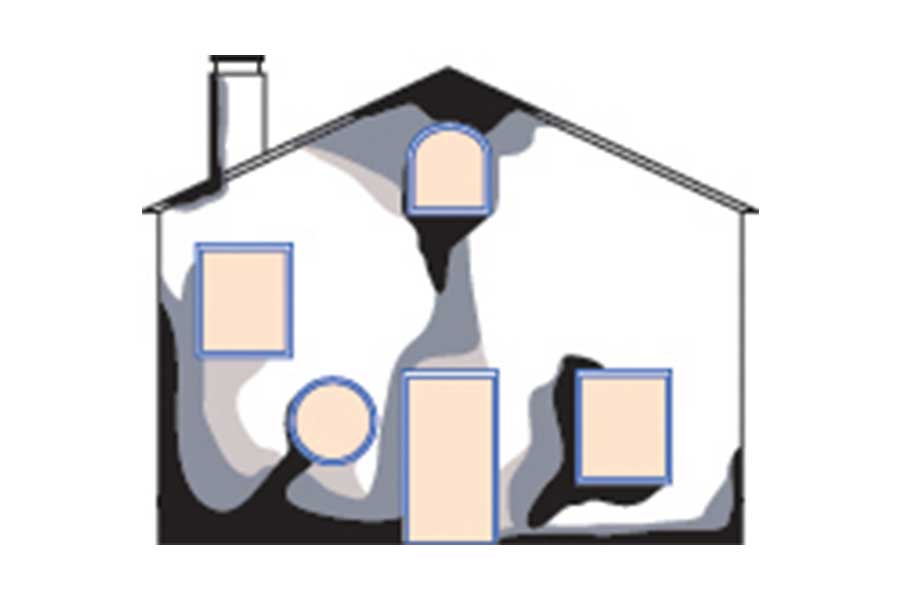
Fig. 2 – Termografia per rilevare la distribuzione dell’umidità (maggiore nelle zone più scure)

Una particolare applicazione della termografia consiste nel rilevare la distribuzione superficiale dell’umidità: riscaldando artificialmente ed omogeneamente la superficie esterna di una muratura, la temperatura raggiunta in ogni elemento superficiale dipende fortemente dal contenuto di umidità localmente presente: l’aumento di temperatura nelle zone più umide sarà minore che in quelle più asciutte, e pertanto una registrazione termografica consente di ricavare una mappatura comparativa dell’umidità superficiale. Sarà poi possibile, con pochi prelievi mirati sulla base delle indicazioni termografiche, determinare in assoluto e con precisione il contenuto di umidità mediante prove di essiccamento dei prelievi in laboratorio. Questo è un tipico esempio per dimostrare la complementarità di una prova non-distruttiva (come la termografia) con una prova distruttiva (come la determinazione dell’umidità in laboratorio per essiccamento dei prelievi).

ENDOSCOPIA

L’endoscopio è uno strumento che consente di vedere in cavità, inaccessibili all’osservazione diretta, attraverso fori (da qualche mm a qualche cm) praticati nella struttura e nei quali passa un sistema ottico di tipo rigido costituito da obiettivi e lenti tradizionali, o di tipo flessibile formato da fibre ottiche. In entrambi i casi, l’apparecchio include anche un sistema di illuminazione interna ed un oculare esterno abbinato ad una camera fotografica per registrare le osservazioni endoscopiche. L’endoscopio consente in sostanza di osservare lo stato delle superfici interne in corrispondenza dei fori praticati nella struttura. Sebbene, a rigore, la prova non sia assolutamente non-distruttiva, in quanto occorre praticare dei fori nella struttura, essa viene così catalogata in quanto è impiegata per diagnosi in sito sulla struttura, molto spesso con successo soprattutto dopo aver effettuato l’indagine termografica a cui viene spesso abbinata.

MAGNETOMETRIA

Questa tecnica consente di individuare materiali ferromagnetici nascosti nella muratura. Il principio del metodo si basa sull’induzione magnetica: se un conduttore elettrico (di lunghezza l) si muove con una velocità v attraverso un campo magnetico di intensità B, all’estremità del conduttore si genera una differenza di potenziale e cosi calcolabile:e = B l vSe le estremità del conduttore in movimento sono collegate con un circuito esterno stazionario rispetto al campo magnetico, la tensione indotta e causa il passaggio di una corrente di intensità i, la quale determina una caduta di potenziale iR, dove R è la resistenza elettrica del conduttore in movimento. La differenza di potenziale V alle estremità del conduttore diventa:V = e – iRIn pratica il magnetometro si compone di una sonda che viene messa in movimento sulla superficie della struttura da indagare. La sonda consiste in una bobina attraversata da una corrente alternata di frequenza costante che genera un campo magnetico alternato. Gli oggetti metallici, incassati nella struttura da indagare, ma tali che si trovino nell’area di influenza del campo magnetico, alterano la differenza di potenziale all’estremità della bobina in base al principio sopra illustrato. L’alterazione del voltaggio viene segnalata su una scala o registrata graficamente (Fig. 3). L’alterazione dipende dallo spessore dell’oggetto metallico e da quello del materiale coprente: nel caso di strutture in cemento armato, per esempio, il magnetometro, adeguatamente tarato, consente di rilevare il diametro dell’armatura in acciaio e lo spessore del copriferro.

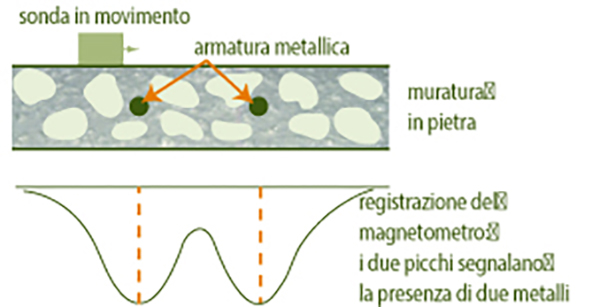
Fig.3 – Esempio di applicazione della magnetometria per rilevare la presenza dei ferri nel solaio in c.a.

GAMMAGRAFIA

Questa tecnica di indagine non-distruttiva, largamente impiegata in altri settori dell’ingegneria meccanica, si basa sulle diverse capacità dei materiali di assorbire energia elettromagnetica emessa da sorgenti radioattive in grado di produrre raggi X. Una pellicola particolare viene impressionata dalle radiazioni che fuoriescono dal manufatto esposto alle radiazioni provenienti dalla sorgente radioattiva: sulla pellicola si evidenziano diverse tonalità di grigio in relazione alle caratteristiche di opacità o trasparenza del manufatto alle radiazioni X.Per quanto molto utile nel segnalare la presenza di elementi metallici, di fessurazioni e di cavità non visibili, la gammagrafia pone qualche problema in relazione alla sicurezzadelle persone direttamente o indirettamente coinvolte nella sperimentazione e pertanto richiede una specifica autorizzazione.

AUSCULTAZIONE SONICA

La tecnica, già utilizzata con successo per il controllo delle fondazioni profonde, si basa fondamentalmente sulla misurazione del tempo impiegato dalle onde soniche – di frequenza compresa tra 16 e 20 kHz nell’attraversare un determinato percorso all’interno di un materiale. Nella Fig. 4 è schematicamente mostrato il principio del metodo nel caso si voglia evidenziare la presenza di una fessura in un palo di fondazione in c.a. attraverso l’auscultazione delle onde soniche: queste, infatti, incontrando una discontinuità del palo (fessura) vengono in parte riflesse ed in parte rifratte. Il trigger fa scattare un contatore di tempo allorquando la sorgente (un martello, un generatore di rumore, ecc.) emette le onde soniche. Il sensore raccoglie l’onda riflessa, la trasforma in un segnale elettrico che interrompe il contatore. La misura del tempo t di percorrenza dell’onda sonica riflessa all’interno del materiale integro (2L₀) e la conoscenza della velocità (V) con cui le onde soniche viaggiano attraverso il materiale permettono di risalire alla lunghezza L₀ in corrispondenza della quale si trova una fessura. Lo stesso principio può essere utilizzato nell’auscultazione sonica per trasmissione: in questo caso la sorgente ed il sensore sono posti, per esempio, sulle due facce opposte di una muratura; muovendo la sorgente ed il sensore lungo l’altezza della muratura è possibile registrare eventuali discontinuità del materiale che compone la struttura (cavità, fessure, eterogeneità, ecc.).

RILEVAMENTO DEGLI ULTRASUONI

Le vibrazioni meccaniche con frequenze superiori a 20 kHz, e fino a 1000 MHz, non sono percepite dall’orecchio umano e sono definite ultrasoniche. Le onde ultrasoniche, a differenza di quelle soniche, non si trasmettono altrettanto facilmente nell’aria; entrambe, però, possono essere molto facilmente trasmesse, anche per lunghe distanze, attraverso materiali liquidi e soprattutto solidi.La specificità delle onde ultrasoniche consiste nel fatto che se esse incontrano uno strato di aria (fessura, cavità, intercapedine) vengono quasi completamente riflesse. Si calcola che è sufficiente una fessura di circa 1 mm per bloccare la trasmissione degli ultrasuoni aventi una lunghezza d’onda di circa 1 mm. La velocità (V) con cui si trasmettono le onde soniche o ultrasoniche è regolata dalla seguente equazione:dove E_d è il modulo elastico dinamico (N/mm²) del materiale attraversato dalle onde ultrasoniche, r è la sua massa volumica (kg/m³), e v è il modulo di Poisson.Se sono noti (o si misurano) i valori di r e di V, si può calcolare E_d dalla misura di V. Se si evidenziano variazioni di V lungo una certa dimensione di una struttura di spessore nominale costante, ciò può essere imputato a variazioni di materiale (variando il materiale varia E_d) oppure a presenza di fessure o di cavità. Come si vede, non è facile emettere una diagnosi di deterioramento sulla semplice rilevazione di questa prova non-distruttiva: tuttavia, come si è già detto, le prove non-distruttive, incluse quelle basate sulla misura di velocità di propagazione degli ultrasuoni, possono segnalare le zone sospettate di essere degradate e permettono pertanto di “mirare” meglio le aree da sottoporre a prelievi per le prove distruttive.Il rilevamento della trasmissione degli ultrasuoni può essere fatto mediante una sorgente di onde con frequenza solitamente compresa tra 50 e 100 kHz, ed una sonda ricevente. Con un cronometro elettronico si misura il tempo impiegato dalle onde a percorrere un determinato cammino di spessore L noto e si calcola quindi la velocità V. Si possono attuare tre tipi di rilevazioni a seconda delle circostanze: trasmissione diretta, semi-diretta, ed indiretta (Fig. 5).

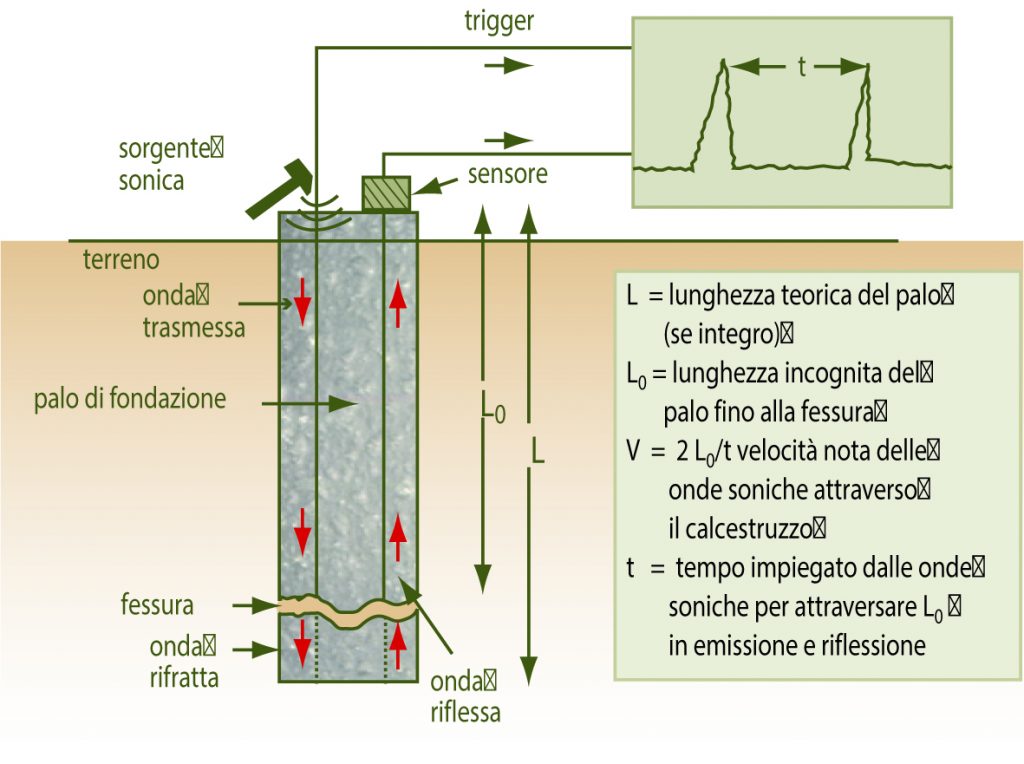
Fig.4 – Rilevamento di una fessura in un palo di fondazione mediante auscultazione sonica.

Fig.5 – Tipi di trasmissione (diretta, indiretta e semi-diretta) degli ultrasuoni realizzati con diversi posizionamenti della sonda di emissione (E) e di ricezione (R) delle onde.

Ovviamente, quando è possibile, la trasmissione diretta è preferibile perché consente una misura dello spessore (L) attraversato dalle onde e quindi, mediante il rilevamento del tempo (t), anche della velocità V e quindi del modulo elastico dinamico E_d. Quando non è possibile posizionare le due sonde in opposizione, si può ricorrere agli atri due tipi di trasmissione che — pur meno precisi perché non si conosce il cammino percorso dalle onde — consentono comunque, attraverso rilevazioni comparative eseguite su strutture analoghe, di evidenziare discontinuità o difetti non visibili direttamente. Per esempio, nella trasmissione indiretta effettuata lungo un muro di spessore (L) si può evidenziare la presenza di anomalie posizionando la sonda di ricezione in punti diversi ed equidistanti tra loro.

SCLEROMETRIA

Le prove sclerometriche, sicuramente le più impiegate tra quelle non-distruttive, consentono di determinare la durezza superficiale di una struttura in calcestruzzo mediante la misura del rimbalzo di un’asta proiettata sulla superficie della struttura stessa. Poiché esiste una qualche correlazione tra la durezza superficiale e la resistenza meccanica, molto spesso lo sclerometro (Fig. 6) è utilizzato per ricavare i valori di resistenza meccanica a compressione. In realtà, la correlazione tra durezza superficiale e resistenza a compressione — e quindi la taratura dello strumento — dipende da alcuni parametri (come la durezza dell’aggregato lapideo, finitura e compattazione dello strato corticale, stagionatura superficiale, ecc.) che possono influenzare la correlazione stessa.

Fig.6 – Impiego dello sclerometro per misurare la durezza superficiale di un pilastro.

Pertanto, il miglior impiego della sclerometria, come avviene tipicamente per le prove non-distruttive, è quello di individuare comparativamente zone di calcestruzzo relativamente più deboli e più forti (in termini di durezza superficiale e quindi di resistenza meccanica), in corrispondenza delle quali con poche e misurate prove distruttive (carotaggio e schiacciamento dei provini) si può determinare, in valore assoluto, la resistenza meccanica o il modulo elastico statico del materiale in sito.

Olistico: approccio nello studio del calcestruzzo

L’approccio olistico, (dal greco hólos che significa che significa “tutto”) è stato proposto prima da Idorn (Concrete Progress. From Antiquity to the Third Millennium, Thomas Telford, London, 1997) e poi più estesamente ripreso da Mehta (Durability – Critical Issues for the Future“, Concrete International, Vol. 19, No. 7 July, 1997, pp 27-35.) per indicare una nuova metodologia finalizzata allo studio della durabilità delle strutture in calcestruzzo. Più in generale, l’approccio olistico, cioè integrale, è stato proposto per contrastare l’eccesso di riduzionismo in ogni campo della scienza e della tecnologia, basato sulla pretesa che tutti gli aspetti di una struttura complicata o di un fenomeno complesso (nell’economia come nella medicina, nell’ingegneria come nella biologia) possano essere compresi riducendoli a parti più semplici. Nel campo del calcestruzzo, con l’approccio riduzionistico si è spesso semplificata la struttura reale riducendola in provini e trasformando il complesso ambiente naturale in un ambiente di laboratorio dove si possa far variare un solo parametro per volta a parità di tutte le altre condizioni. Questo procedimento analitico è figlio del moderno pensiero scientifico, e si è rivelato molto utile per lo sviluppo di nuove teorie scientifiche come anche per la realizzazione di tecnologie molto progredite. Tuttavia, l’eccesso di riduzionismo può essere fuorviante nello studio di sistemi molto complessi per i quali l’approccio olistico, basato sull’intuizione, si può rivelare più proficuo. Anzi, secondo Capra (The Turning Point, Batan New Ages Book, 1983.), i due approcci debbono essere considerati complementari.A differenza dell’approccio riduzionistico, che consente di misurare con precisione i parametri studiati e di elaborare talvolta anche un modello matematico per descriverne il comportamento in ben determinate condizioni, l’approccio olistico è necessariamente qualitativo o al massimo semi-quantitativo, ma non per questo meno proficuo o vantaggioso rispetto all’approccio riduzionistico. Per quanto riguarda il calcestruzzo, un paio di esempi potranno essere utili per esaminare i vantaggi dell’approccio riduzionistico o di quello olistico per affrontare i vari problemi.

L’APPROCCIO RIDUZIONISTICO

Il primo esempio riguarda lo studio della resistenza meccanica a compressione (R_c). Come è noto, R_c dipende, oltre che dal rapporto acqua/cemento (a/c), da molti altri parametri: grado di compattazione del calcestruzzo dentro i casseri, temperatura e umidità relativa della stagionatura, tempo di maturazione, forma geometrica e dimensione dei provini, tipo e classe di cemento, e porosità degli aggregati lapidei. Per semplificare un così complesso sistema, con un approccio riduzionistico occorre ridurlo in parti più semplici facendo variare, per esempio solo a/c e misurando R_c mantenendo costanti tutti gli altri parametri. Qualcosa del genere dovette fare Abrams per ricavare la famosa legge che porta il suo nome:R_c = K₁/K₂/^a/c_[1]dove K₁ e K₂ sono due costanti che dipendono da tutti gli altri parametri tenuti costanti (tempo di rottura, temperatura di stagionatura, tipo di cemento, forma geometrica dei provini, ecc.). Per arrivare all’equazione [1] o altre simili, si può cominciare a preparare in laboratorio una serie di calcestruzzi con lo stesso tipo di cemento dove l’unico parametro variabile è il valore di a/c e procedere quindi ad una completa e costante compattazione del calcestruzzo fresco, ad una stagionatura umida sempre a 20°C, ad una rottura a compressione dei provini cubici sempre a 28 giorni. Quindi, nota la resistenza R_c per ogni valore di a/c, si potranno ricavare le costanti K₁ e K₂ oppure si potrà rappresentare graficamente l’equazione [1] a 28 giorni (Fig. 1).

Fig. 1 – Influenza del rapporto acqua-cemento (a/c) sulla resistenza caratteristica (R_ck) del calcestruzzo con CEM II B/L 32.5R.

Ripetendo l’esperienza alla stessa temperatura, impiegando lo stesso cemento, e rompendo i provini ad un’altra stagionatura – per esempio a 7 giorni – si potranno calcolare altri valori di K₁ e K₂. Procedendo in questo modo ad altre stagionature (per esempio 1 e 3 giorni) sarà possibile offrire un quadro più completo della correlazione R_c – a/c a tempi diversi ma riferiti alla stessa temperatura, stesso cemento e stesso grado di compattazione. Per le strutture reali, però, difficilmente si conoscono il grado di accuratezza adottato nel compattare il calcestruzzo gettato nei casseri, la temperatura effettiva (tra l’altro mai costante, ma variabile di giorno in giorno in base al clima ed al calore di idratazione sviluppato inizialmente). Pertanto, l’equazione di Abrams non può essere molto precisa per predeterminare la R_c del calcestruzzo nelle strutture reali, noti i valori di acqua e cemento immessi in betoniera o, al contrario, per calcolare il valore di a/c adottato in base alla misura della R_c su una “carota” estratta dalla struttura. Tutto ciò non significa però che uno studio affrontato con l’approccio riduzionistico sia di scarsa utilità, ma piuttosto che i risultati ottenuti non possano essere estrapolati al di fuori delle limitazioni entro le quali furono ricavati.Per tornare all’equazione di Abrams [1], si possono segnalare almeno due utili applicazioni pratiche. La prima riguarda la necessità di controllare la qualità del calcestruzzo, ed in particolare la sua resistenza meccanica, attraverso la misura di R_c non già sulle strutture, ma su provini di geometria nota, compattati a rifiuto, e stagionati a temperature e per tempi ben standardizzati (20°C e 28 giorni). Solo in questo modo il valore di R_c è significativo ed esprime la potenziale qualità del calcestruzzo utilizzato in cantiere sulla base di precise prescrizioni: esso è utile, quindi, per regolare le forniture del produttore di calcestruzzo all’impresa, ma non può essere esteso, salvo eccezioni, al controllo della resistenza del calcestruzzo delle strutture. La seconda applicazione, molto più utile per il progresso tecnologico, riguarda l’insegnamento derivante dalla legge di Abrams: una volta noto l’importante ruolo giuocato da a/c, si è compresa l’importanza di controllare l’acqua introdotta nell’impasto (compresa quella derivante dall’umidità degli aggregati dalla cui variabilità può dipendere molto la scarsa riproducibilità dei risultati di R_c). Inoltre, dalla legge di Abrams deriva tutta la ricerca che ha portato all’invenzione ed allo sviluppo di additivi sempre più efficaci nel ridurre l’acqua di impasto, e conseguentemente il valore di a/c, senza penalizzazione della lavorabilità.

L’APPROCCIO OLISTICO

Il secondo esempio riguarda lo studio della durabilità delle strutture reali (travi, pilastri, solette, ecc.) che risulta essere molto più complesso di quello affrontabile in laboratorio. Quest’ultimo viene studiato necessariamente con un approccio riduzionistico preparando alcune serie di provini per ciascuna delle quali si fa variare un solo parametro; (per esempio a/c, oppure il tipo di cemento, oppure la temperatura di esposizione, oppure ancora la concentrazione di agente aggressivo). Questo approccio semplifica lo studio perché consente di determinare l’influenza di ciascun parametro sulla durabilità a parità di tutte le altre condizioni.Tuttavia, occorre estendere con molta prudenza i risultati ottenuti con l’approccio riduzionistico alle strutture reali. Per esempio, sovente si verifica che due parti molto prossime nella stessa struttura – quindi a parità di a/c, di compattazione, ed apparentemente di tutti gli altri parametri – presentino comportamenti di durabilità molto diversi tra loro, difficilmente interpretabili sulla base del solo studio riduzionistico di laboratorio. L’approccio olistico, basato soprattutto sull’osservazione comparativa ed acuta delle strutture reali danneggiate e di quelle integre della stessa opera, consente invece di arrivare ad una comprensione intuitiva del fenomeno ancorché difficilmente modellabile in termini quantitativamente analitici.La Fig. 2 illustra in modo sintetico e semi-quantitativo i principali parametri responsabili del degrado di una struttura in calcestruzzo armato (4). Questi parametri sono raggruppabili in tre categorie:– porosità del materiale– umidità delle strutture– esposizione ad ambiente aggressivoFig. 2 – Approccio olistico al degrado: occorre la coesistenza di umidità, di porosità del materiale e di agenti aggressivi nell’ambiente perché si manifesti il degrado (area rossa).Ciascuna categoria di parametri è rappresentata da un cerchio in Fig. 2. Solo quando tutte e tre le categorie coesistono, alternativamente o continuamente, si può manifestare il degrado: questa situazione corrisponde alla sovrapposizione dei tre cerchi ed è rappresentata dalla zona centrale del diagramma ternario di Fig. 2. La sovrapposizione di soli due cerchi che corrisponde alla coesistenza di due categorie di parametri, per esempio ambiente umido ed aggressivo per presenza di solfati, non comporta alcun rischio di degrado per la mancanza della terza categoria di parametri, cioè della porosità del calcestruzzo. Naturalmente, ancora meno probabile è il rischio di degrado in presenza di una sola categoria di parametri: per esempio calcestruzzo poroso in ambiente asciutto e privo di agenti aggressivi.Nella Fig. 2 sono anche mostrati i vari parametri appartenenti a ciascuna categoria. Per esempio, la porosità del calcestruzzo include un numero significativo di parametri che possono influenzare direttamente o indirettamente la porosità: non solo il valore di a/c che, come è noto dalla teoria di Powers, influenza la porosità capillare (1-100 mm) della matrice cementizia; ma anche una carente stagionatura umida iniziale, l’esposizione alle escursioni igro-termiche dell’ambiente che possono provocare la formazione di microfessure (100-300 mm) attraverso le quali l’acqua ambientale può penetrare trasportando gli agenti aggressivi ed aggirando una matrice cementizia anche poco porosa per il basso valore di a/c. Ed ancora: uno scarso grado di compattazione del calcestruzzo nella struttura reale, in relazione ad un impasto segregabile, poco lavorabile e/o poco vibrato (si veda l’articolo “Lavorabilità del calcestruzzo fresco: influenza sul calcestruzzo in servizio” disponibile sul sito www.encosrl.it è l’ ABC del calcestruzzo:), può provocare la presenza di macrovuoti (1 mm – 1 cm), talvolta fino alla formazione di vistosi “vespai”, che ovviamente facilitano l’ingresso dell’acqua e degli agenti aggressivi anche in calcestruzzi confezionati con basso a/c e ben stagionati a umido.Per quanto riguarda l’aggressività dell’ambiente ci si può limitare all’elenco degli agenti aggressivi più frequentemente riscontrabili e previsti dalla normativa europea (si consulti l’articolo “Durabilità del calcestruzzo armato” sul sito www.encosrl.it è l’ABC del calcestruzzo:): solfati, cloruri, alcali, ossigeno, anidride carbonica, ghiaccio, tenendo presente che molto spesso questi fattori agiscono contemporaneamente con effetti talvolta sinergici (1 + 1 = 3).

IL RUOLO DELL’ACQUA

L’acqua, infine, giuoca un ruolo determinante innanzitutto nel trasporto degli agenti aggressivi dall’ambiente verso i singoli componenti delle strutture (armature metalliche, pasta cementizia ed aggregati), e, nel caso di ambienti molto freddi (< 0°C), essa stessa diventa l’agente aggressivo attraverso la formazione di ghiaccio. Ma l’aspetto più complesso, nel ruolo giuocato dall’acqua, riguarda la presenza continua o intermittente che, a seconda dello specifico meccanismo di degrado, può diventare l’elemento determinante per promuovere o bloccare il fenomeno del deterioramento delle strutture. Per esempio, nel caso della corrosione dei ferri di armatura promossa da carbonatazione è essenziale che il calcestruzzo sia esposto alla presenza intermittente dell’acqua (Fig. 3) per favorire, nei periodi asciutti il trasposto dell’aria. Questa con la presenza di anidride carbonica (CO₂) neutralizza la calce e con la presenza di ossigeno (O₂) alimenta la formazione di ruggine. In strutture permanentemente immerse in acqua, invece, il fenomeno della corrosione è di fatto bloccato per la difficoltà dei gas CO₂ e O₂ a diffondere attraverso il copriferro satura di acqua.

Fig.3 – Struttura in calcestruzzo armato con espulsione del copriferro a seguito della formazione di ruggine (più voluminosa dell’acciaio) sulla superficie delle armature metalliche corrose per carbonatazione.

Fig.4 – Fessurazione da reazione alcali-aggregato in un pavimento di calcestruzzo.

Al contrario, nel caso del degrado dovuto, per esempio, alla reazione alcali-aggregato (Fig. 4) la presenza continua di umidità accelera il decorso del fenomeno purché, ovviamente, siano presenti le altre due condizioni indispensabili al decorso del processo: silice reattiva negli aggregati ed elevata concentrazione di alcali nel calcestruzzo (espressi come Na₂O_eq^* > 2 Kg/m³). Quest’ultima situazione può essere determinata da un eccessivo contenuto di sodio e potassio all’interno del calcestruzzo (cemento con Na₂O > 0.6%) oppure dall’esposizione del calcestruzzo in servizio ad un ambiente esterno ricco di alcali, come avviene per esempio nelle pavimentazioni esposte a salatura (con NaCl) nei periodi invernali per sciogliere il ghiaccio.Una situazione analoga si presenta nell’attacco solfatico con formazione di ettringite: esiste la possibilità che il solfato provenga dall’ambiente esterno (terreni o acque solfatiche) al quale il calcestruzzo è esposto (Fig. 5), oppure che esso sia presente all’interno stesso del calcestruzzo per il lento rilascio (Fig. 6) da uno dei suoi ingredienti solidi (aggregati o cemento). L’attacco solfatico interno, più noto con il nome di DEF (Delayed Ettringite Formation), si è manifestato solo recentemente (anni ’80 e ’90) ed ha colpito in modo particolare alcune tipologie strutturali (traversine ferroviarie in c.a.p.) piuttosto che altre.

Fig.5 – Distacco superficiale del calcestruzzo delle pareti di un canale bagnato da acque solfatiche.

Fig.6 – Esempio di attacco solfatico interno (DEF) nel calcestruzzo di una traversina in c.a.p.: l’eccessivo stato di coazione provoca le microfessure e promuove l’attacco solfatico.

Proprio adottando l’approccio olistico (“Damage by Delayed Ettringite Formation., A Holistic Approach and New Hypothesis“, Concrete International, Vol. 21, No.1, January, 1999, M. Collepardi, pp 69-74) tenendo conto cioè dei vari parametri progettuali, produttivi, composizionali ed ambientali (sollecitazioni a fatica in servizio, microfessure provocate dalle sollecitazioni di precompressione, tipo di cemento impiegato, ciclo termico di maturazione accelerata a vapore, ecc.) è stato possibile risalire alle possibili cause di degrado provocate dall’attacco solfatico interno e le ragioni per le quali le traversine ferroviarie sono più vulnerabili all’attacco solfatico rispetto ad altre strutture (www.encosrl.it è ABC del calcestruzzo :”Ettringite: Dr Jekyll e Mr. Hyde”).*NOTANa₂O_eq=alcali totali espressivi come Na₂O equivalente = Na₂O + 0.66K₂O

Porosità e permeabilità del calcestruzzo

Quanti tipi di pori nel calcestruzzo

Il calcestruzzo, almeno quello convenzionale tradizionalmente impiegato nelle opere dell’architettura e dell’ingegneria civile, è un materiale poroso. Come in tutti i materiali da costruzione, la porosità condiziona le proprietà ingegneristiche, ed in particolare influenza la resistenza meccanica, il modulo elastico, la permeabilità e la durabilità.Nel caso del calcestruzzo, la porosità può essere di cinque tipologie:- quella dovuta alla insufficiente compattazione del conglomerato e quindi alla incompleta espulsione di aria intrappolata dalla malta del calcestruzzo fresco; si tratta dei macrovuoti visibili ad occhio nudo da circa 1 mm a qualche decina di mm;- la porosità eventualmente presente all’interno degli aggregati lapidei, per una massa volumica apparente inferiore a quella assoluta, e che può raggiungere una frazione ragguardevole nei cosiddetti inerti leggeri (Fig. 1) con miglioramento delle proprietà termoisolanti ed una penalizzazione delle prestazioni meccaniche.Fig. 1 – Presenza di vuoti nell’interno di inerti leggeri.– la porosità eventualmente generata dall’inglobamento di aria, in forma di microbolle sferiche di circa 100-300 m m visibili al microscopio ottico (Fig. 2), grazie alla presenza di additivi aeranti per assicurare un’adeguata resistenza alla formazione di ghiaccio in servizio;- la porosità presente tra le particelle che compongono la pasta di cemento come pori di forma irregolare, con dimensione compresa tra 0,1 m m e 10 m m e visibili al microscopio elettronico (Fig. 3), nota come porosità capillare e fortemente correlata con la composizione e la stagionatura del calcestruzzo;- quella presente all’interno dei prodotti idratati solidi, ed in particolare del C – S – H detto in passato gelo tobermoritico, nota come porosità del gel, con dimensione di 1-10 nm, non visibile anche con il microscopio elettronico, ma determinabile indirettamente attraverso misure di adsorbimento di sostanze gassose come azoto, elio, o vapore acqueo (Fig. 5).Fig. 2 – MIcrobolle (100-300 mm) d’aria inglobata nella malta che avvolge gli aggregati grossi (microscopia ottica).Fig. 3 – Porosità capillare nella pasta cementizia (microscopia elettronica).

Porosità capillare e resistenza meccanica

La porosità del gel è allocata dentro le particelle solide che formano la pasta di cemento, mentre la porosità capillare è presente tra queste particelle solide (Fig.3). La porosità del gel ammonta al 28% del volume occupato dalle particelle solide della pasta cementizia e non può essere sostanzialmente modificata. Al contrario, la porosità capillare può essere significativamente modificata attraverso il rapporto acqua-cemento (a/c) e/o il grado di idratazione (a ), cioè la frazione di cemento idratato. La dipendenza della porosità capillare da questi due parametri è stata matematicamente quantificata con la teoria di Powers (Scienza e Tecnologia del Calcestruzzo, Mario Collepardi, pg 148-151, 3^ ed., Hoepli, Milano, 1990):V_p = 100 a/c – 36.15 a [1]dove V_p è il volume dei pori in litri per ogni 100 Kg di cemento. Se si vuole ridurre la porosità capillare occorre ridurre il rapporto acqua-cemento e/o aumentare il grado di idratazione; è possibile annullare, almeno in teoria, la porosità capillare: per esempio secondo la [ 1] con a/c = 0.3615 ed a = 1, V_p diventa zeroPowers ha elaborato, con un suo modello matematico, una relazione per quantificare l’influenza della porosità capillare (V_p) sulla resistenza meccanica a compressione (R_c) in assenza di macrovuoti dovuti a incompleta compattazione:[2] dove V_g è il volume del cemento idratato per ogni 100 Kg di cemento anidro, ed R_c eguaglia la costante K (che vale 250 MPa) quando V_p è nullo. A questa elevata prestazione meccanica ci si può avvicinare moltissimo con l’adozione di bassi rapporti acqua-cemento e l’impiego di additivi superfluidificanti per compattare completamente il conglomerato. Sempre secondo la teoria di Powers, V_g è così calcolabileV_g = 67.90 a [3]Secondo l’equazione [3] il volume del cemento idratato V_g è di 67.90 litri, per ogni 100 Kg di cemento, a idratazione completa (a =1) ed assume valori proporzionalmente crescenti all’aumentare di a tra zero (inizio impasto) ed 1. Inserendo le equazioni [1] e [3] all’interno della [2] si ottiene:[4]Fig.4 – Schematizzazione dei pori del gel dentro una particella di cemento idrato e dei pori capillari tra le particelle di cemento idratatoL’equazione [ 4] significa che per aumentare R_c si può agire su due fronti:- occorre innanzitutto diminuire a/c (che appare al denominatore), cioè ridurre l’acqua di impasto a parità di dosaggio di cemento, senza però aumentare il volume di macrovuoti legati ad una maggiore difficoltà di compattare il calcestruzzo fresco (da questo punto di vista l’adozione di un basso rapporto acqua-cemento comporta in pratica l’impiego di additivi fluidificanti e superfluidificanti capaci di compensare la minore lavorabilità del calcestruzzo fresco derivante alla riduzione dell’acqua di impasto);- si può anche aumentare R_c, per un dato a/c, aumentando il grado di idratazione a (che “pesa” più al numeratore che non al denominatore), cioè prolungando il tempo di stagionatura e/o scegliendo cementi più reattivi.Porosità capillare e modulo elasticoAttraverso un’equazione del tutto analoga alla [2] con un valore per la costante K ovviamente diverso. Al pari della resistenza meccanica anche il modulo elastico (E) è influenzato dalla porosità capillare

Porosità capillare e permeabilità

La permeabilità di un fluido attraverso un solido poroso diventa possibile solo se i pori sono tra loro connessi (porosità continua). Nel caso del calcestruzzo, ed in particolare della sua permeabilità all’acqua, la porosità discontinua, e quindi l’impermeabilità, è assicurata solo al di sotto di una certa soglia della porosità capillare: questa corrisponde, per ogni determinato valore di a/c, ad un certo grado di idratazione a raggiungibile dopo un determinato tempo di stagionatura (Tabella 1). I dati della Tabella 1 indicano che più elevato è a/c, più lungo deve essere il tempo di stagionatura (e quindi maggiore il grado di idratazione a ) perché il calcestruzzo diventi impermeabile: per esempio, con a/c di 0.55 occorrono 28 giorni per conseguire l’impermeabilità del calcestruzzo; se però si adotta un rapporto acqua-cemento di 0.45 è sufficiente appena una settimana per raggiungere lo stesso obiettivo; d’altra parte con a/c molto elevato (³ 0.70) non è mai possibile conseguire l’impermeabilità del calcestruzzo.

a/c	TEMPO
0.40	3 giorni
0.45	1 settimana
0.50	2 settimane
0.55	1 mese
0.60	6 mesi
0.70	1 anno
>0.70	infinito

Tabella 1 – Tempo richiesto per la impermeabilizzazione del calcestruzzo in relazione al rapporto a/cDa un punto di vista pratico la situazione di impermeabilità viene valutata (UNI EN 12390-8) sottoponendo un provino prismatico di calcestruzzo ad acqua sotto pressione per 3 giorni alla pressione di 7 bar): il calcestruzzo è considerato impermeabile se, dopo questi 3 giorni, l’acqua non ha penetrato il materiale per più di 20 mm per effetto del conseguimento della porosità discontinua.

Porosità capillare e durabilità

Anche la durabilità è fortemente influenzata dalla porosità capillare oltre che dagli altri tipi di porosità. La durabilità dipende in generale dalla porosità, tuttavia la relazione tra le due grandezze è funzione del tipo di porosità. In linea di massima si può affermare che la porosità continua nuoce alla durabilità, mentre quella discontinua, purché distribuita in una matrice densa e poco porosa, è ininfluente o giova alla durabilità. Per esempio, i macrovuoti dovuti a difetti di compattazione del calcestruzzo fresco potrebbero collegare i ferri di armatura con l’ambiente esterno e costituiscono, pertanto, un sistema di pori altamente pericolosi per l’integrità della struttura.Un altro tipo di porosità continua capace di favorire l’accesso di agenti ambientali aggressivi (aria, umidità, cloruri, ecc.) è costituita dalla porosità capillare (Fig. 4). Per un calcestruzzo privo di macrovuoti dovuti ad imperfetta compattazione, la durabilità del calcestruzzo nei confronti di un ambiente aggressivo può essere migliorata riducendo il volume V_p della porosità capillare per ostacolare la penetrazione dell’acqua, e quindi impedire l’ingresso degli agenti aggressivi all’interno del calcestruzzo veicolati dall’acqua. Da un punto di vista pratico, il volume della porosità capillare viene ridotto – equazione [ 1] – riducendo a/c, come appare chiaramente in tutte le raccomandazioni sulla durabilità (consultare l’articolo “Durabilità del calcestruzzo armato sul sito www.encosrl.it è l’ABC del calcestruzzo) e garantendo un minimo di stagionatura umida (3-7 giorni) per assicurare un livello accettabile del grado di idratazione (a).Un tipo di porosità indifferente alla durabilità del calcestruzzo è costituito dal sistema di pori contenuti all’interno degli inerti leggeri (Fig. 1): in questo caso la durabilità della struttura non risente minimamente della porosità degli aggregati, giacché l’ingresso degli agenti aggressivi, dall’ambiente all’interno del calcestruzzo, è governato dalla porosità capillare e dai macrovuoti (per insufficiente compattazione) distribuiti nella matrice cementizia che avvolge gli aggregati.Una porosità altamente benefica alla durabilità del calcestruzzo è rappresentata dalle microbolle d’aria (Fig. 2) non collegate tra loro, cioè disperse discontinuamente in una matrice cementizia con bassa porosità capillare. La presenza di microbolle di aria inglobata (grazie alla presenza di agenti aeranti capaci di modificare la tensione superficiale dell’acqua) è da tempo riconosciuta come essenziale alla produzione di calcestruzzi durabili esposti in servizio ai climi invernali (cicli di gelo-disgelo). Infatti, l’acqua contenuta nei pori capillari, e non ancora congelata, è sospinta nelle microbolle d’aria con allentamento delle tensioni che insorgono quando si forma il ghiaccio con aumento di volume rispetto all’acqua liquida. In assenza delle microbolle d’aria, l’acqua dei pori capillari non ancora congelata è sospinta da una pressione idraulica che insorge per l’aumento di volume che accompagna la formazione dei primi cristalli di ghiaccio (si consulti l’articolo “ Gelo e disgelo del calcestruzzo” disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo). Affinché le microbolle d’aria possano effettivamente allentare le tensioni insorte per la formazione del ghiaccio, è necessario che non siano molto distanti tra loro: la reciproca distanza (spacing) non deve superare 300-400 m m. Per concludere, un sistema di vuoti particolarmente favorevole al calcestruzzo durabile in qualsiasi clima, ed in particolare negli ambienti molto aggressivi (gelo-disgelo, sali disgelanti, ambiente marino, ecc.) è rappresentato da una matrice cementizia con una porosità capillare discontinua e quindi impermeabile (tipicamente raggiungibile dopo 1 mese di stagnatura con a/c = 0.55) nella quale siano disposte microbolle d’aria (100-300 m m) ben spaziate tra loro con una distanza di circa 300 m m.

Qualità del calcestruzzo

Costanza di qualità del calcestruzzo

Il concetto di “qualità“, o più precisamente di costanza di qualità, è stato ampiamente recepito in Italia nel decennio del 1990 in tutti i settori produttivi di beni materiali o di servizi. Nella normativa UNI EN ISO 8402 del Giugno 1992 la qualità era definita come la conformità agli obiettivi prefissati ed ai requisiti concordati con i clienti, principio di base rimasto sostanzialmente invariato nelle attuali norme della famiglia UNI EN ISO 9000.Per rimanere nel settore della terminologia sulla qualità, e prima ancora di entrare nel merito su come perseguire la costanza di qualità nel settore del calcestruzzo, è opportuno chiarire il significato di:– Certificazione di prodotto– Certificazione del sistema qualità– Manuale di qualità– Guide applicativeSecondo le norme della famiglia ISO 9000 la Certificazione di Prodotto, verificata da un Istituto di Certificazione, garantisce che il prodotto certificato soddisfa i requisiti di accettabilità definiti dalle specifiche tecniche. Questo tipo di certificazione offrirebbe al committente (impresa), che volesse, per esempio, acquistare calcestruzzo preconfezionato o elementi prefabbricati, la garanzia che le caratteristiche di ogni singolo prodotto o fornitura siano rispondenti ai limiti di accettabilità correlate con l’esigenza dell’opera nel suo insieme.Mentre per quasi tutti i componenti del calcestruzzo e molti dei prodotti premiscelati o prefabbricati in conglomerato cementizio esiste ormai una certificazione di prodotto regolamentata da una specifica norma europea armonizzata, lo stesso obbligo cosa non è ancora vigente per il calcestruzzo. La norma europea UNI EN 206 contenente le regole per la produzione ed il controllo di produzione del calcestruzzo, continua infatti ad essere una semplice norma volontariaCertamente anche per la produzione del calcestruzzo si potrà applicare la Certificazione del Sistema di Qualità che in realtà, rispetto alla Certificazione di Prodotto, offre al committente molte minori garanzie sulla effettiva costanza di qualità. Infatti la Certificazione del Sistema di Qualità, anch’essa verificata da un Istituto di Certificazione, garantisce soltanto che l’azienda produttrice agisce nel rispetto di alcune regole di comportamento descritte nel Manuale di Qualità, documento pubblico ed esigibile dai committenti, dove l’azienda dichiara i propri obiettivi e le propria organizzazione per applicare il suo specifico Sistema di Qualità.Per fare un esempio estremo ed improbabile, un’azienda di calcestruzzo preconfezionato potrebbe porsi come obiettivo nel suo Sistema di Qualità, di far eseguire dal conducente dell’autobetoniera un giro di valzer della durata di 60 secondi al termine del carico del veicolo e prima di partire per il cantiere. L’Istituto di Certificazione potrebbe in effetti garantire che l’azienda produttrice agisce in perfetto accordo alla procedura descritta dal Manuale di Qualità per quanto attiene al giro di valzer. Questo esempio (ripetiamo estremo ed improbabile) serve ad illustrare che la Certificazione del Sistema di Qualità è ben diversa, ed ovviamente meno significativa per la costanza di qualità, che non la Certificazione di Prodotto.A livello nazionale, tuttavia, le Linee Guida per il calcestruzzo preconfezionato del Consiglio Superiore del LL.PP: richiamate anche nelle Norme Tecniche per le Costruzioni hanno di fatto introdotto un controllo del processo produttivo certificato da un ente terzo notificato simile a quello applicato per la marcatura CE di altri prodotti da costruzione.Proprio per colmare la lacuna esistente tra i due tipi di certificazione, alcuni Istituti di Certificazione hanno emesso e fatto adottare le Guide Applicative che introducono delle prescrizioni particolari, in relazione a determinate specifiche di riferimento, e fissano i requisiti minimi di accettabilità. In sostanza se un’azienda ha adottato le Guide Applicative è possibile, dalla lettura di questo documento come anche del Manuale di Qualità, quantificare quale sia il grado di prestazione minima garantita nella fornitura del calcestruzzo o nell’acquisto di un elemento prefabbricato.Per entrare nello specifico tecnico della produzione del calcestruzzo, di seguito sono esaminati i parametri di processo che più significativamente possono influenzare la costanza di prestazioni del prodotto, queste ultime intese come classe di resistenza (R_ck) e classe di consistenza (slump).I parametri che verranno nel seguito esaminati, anche per ragioni di brevità, riguardano tutte le caratteristiche dell’inerte ed in particolare:– umidità– assorbimento– diametro massimo– granulometria

L’umidità dell’inerte

Il parametro che presenta la maggiore incidenza sulla costanza di qualità del calcestruzzo, in termini di R_ck e di slump, è rappresentato dall’umidità dell’aggregato. Questa, infatti, può radicalmente modificare l’acqua di impasto (a) realmente immessa nel calcestruzzo e quindi, attraverso questa variazione, può provocare modifiche nella lavorabilità che dipende proprio dal valore di a (si consulti sul sito www.encosrl.it è l’ABC del calcestruzzo l’articolo “ Acqua del calcestruzzo: fatti e misfatti sui cantieri). L’influenza della umidità dell’inerte sulle proprietà del calcestruzzo, attraverso le variazioni di a e di a/c, è piuttosto complessa e deve tener anche conto dell’umidità capace di saturare la porosità aperta dell’aggregato definita come assorbimento.L’umidità (u) viene determinata misurando la diminuzione percentuale di massa, a seguito del riscaldamento a 105°C per essiccare completamente il materiale, rispetto alla massa dell’aggregato completamente secco:

	m – m_o
u =	————–	100
	m_o

dove m ed m_o sono rispettivamente la massa dell’aggregato così come disponibile e quella dell’aggregato completamente essiccato.L’assorbimento è quella particolare umidità (u_a) che si trova nell’aggregato quando si trova ad essere saturo a superficie asciutta, s.s.a. (Fig. 1):

	m_s.s.a. – m_o
u_a =	————–	100
	m_o

dove m_s.s.a. è la massa dell’aggregato conservato sotto acqua fino a completa saturazione ed asciugato in superficie.Nella Fig. 1 sono rappresentate schematicamente le quattro possibili situazioni nelle quali può trovarsi un aggregato nei confronti del contenuto di umidità (u): asciutto, insaturo, s.s.a. e bagnato.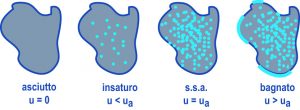

Fig. 1 – Aggregato con umidità interna (area punteggiata) e superficiale (area scura sull’aggregato bagnato)

Influenza dell’umidità dell’inerte sulle prestazioni del calcestruzzo

Nella pratica di cantiere l’aggregato si troverà spesso nella situazione di insaturo, qualche volta (dopo una pioggia) in quello di bagnato, raramente in quella di asciutto (dopo lunga permanenza in clima secco, caldo e ventilato), ed ancor più raramente, e solo transitoriamente, in quella di s.s.a. La condizione di s.s.a. tuttavia, è di grande importanza pratica oltre che teorica, perché è quella in cui vengono a trovarsi gli inerti all’interno del calcestruzzo subito dopo l’impasto, ed è anche la situazione in cui si calcola la massa volumica (peso specifico) della sabbia e della ghiaia per tramutare i volumi dei singoli inerti nelle corrispondenti masse (si veda l’articolo “Mix-Design del calcestruzzo sul sito www.encosrl.it è l’ABC del calcestruzzo). In altre parole un inerte bagnato cede l’acqua in eccesso (u>u_a) rispetto alla situazione di s.s.a. che va a sommarsi all’acqua introdotta in betoniera, facendo aumentare il valore dell’acqua totale di impasto (a). D’altra parte, un inerte insaturo (u<u_a) ed ancor più un inerte asciutto (u=0) comporterà una suzione di acqua da parte dell’inerte fino a portare l’inerte stesso in condizione di s.s.a. con conseguente diminuzione della effettiva acqua di impasto. Le conseguenze di questi scambi di acqua tra inerti e calcestruzzo sono schematicamente sintetizzate in Fig. 2. Per prevenire queste oscillazioni nelle prestazioni del calcestruzzo (R_ck e slump) è necessario compensare le variazioni di umidità apportate o sottratte dall’inerte rispettivamente con minori o maggiori aggiunte di acqua in betoniera. A tale scopo è necessario controllare quasi quotidianamente l’umidità (u) degli inerti (soprattutto in relazione alle variazioni igrometriche dell’ambiente) e tenere sotto controllo il valore dello assorbimento (u_a) soprattutto in relazione ai cambi di cava e quindi di porosità della roccia minerale caratteristica dell’inerte.

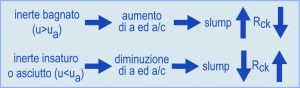Fig.2 – Influenza dell’umidità dell’inerte (u) sull’acqua.

Modifica delle pesate degli ingredienti rispetto al mix-design

Nel seguito è descritto un esempio numerico per le variazioni nelle pesate degli ingredienti, a parità di diametro massimo della ghiaia, rispetto a quelle desunte dal mix-design, a seguito dei controlli di u ed u_a.Mix-design:

c = 300 kg/m³	=====>		=> a/c = 0,67 => R_ck = 25 MPa
a = 134 kg/m³
g = 1122 kg/m³		a = 200 => slump = 150 mm
s = 844 kg/m³

u_g = 3%I valori delle masse g (ghiaia) ed s (sabbia) sono riferiti come al solito alla situazione standard di s.s.a.. Si supponga che in seguito ad una giornata di pioggia, le umidità della ghiaia (u_g) e della sabbia (u_s) risultino:u_s = 6%a fronte di valori di assorbimento costanti che sono:u_ga = 1%u_sa = 0,5%.Essendo per entrambi gli inerti l’umidità maggiore dell’assorbimento si verificherà una cessione di acqua all’impasto da parte degli inerti bagnati. La quantità di acqua ceduta dalla ghiaia è:101 : 103 = 1100 : g’(ssa) : bagnata = (ssa) : (bagnata)dove:- 101 è la massa di ghiaia in ssa per 100 kg di ghiaia secca (questo è infatti il significato di u_ga = 1% secondo l’equazione [1])- 103 è la massa di ghiaia bagnata per 100 Kg di ghiaia secca (questo è infatti il significato di u_g = 3% secondo l’equazione [2])- 1100 è la massa di ghiaia s.s.a. per 1 m³ di calcestruzzo secondo il mix-design, cioè g;– g’ è la massa di ghiaia come disponibile (cioè bagnata) che dovremo introdurre in 1 m³ di impasto per assicurare la presenza di 1100 kg/m³ di ghiaia in condizione di s.s.a. come richiesto dal mix-design.Calcolando g’ attraverso la proporzione [3] si ottiene:g’ = g (103/101) = 1100 ( 103/101) = 1122 kg/m³In altre parole occorre pesare 1122 Kg di ghiaia bagnata per introdurre 1100 Kg di ghiaia s.s.a. come da mix-design; la differenza 1122-1100 = 22 Kg rappresenta l’acqua introdotta surrettiziamente attraverso la ghiaia bagnata.Applicando gli stessi calcoli alla sabbia anch’essa bagnata (s’) si ottieneS1 = S (106/100.5) = 800 (106/100.5) = 844 844 kg/m³22 + 44 = 66 kg/m³ Anche in questo caso è necessario introdurre più sabbia bagnata (844 Kg) per assicurare la presenza di 800 Kg di sabbia in condizione di s.s.a.. La differenza 844-800 = 44 Kg rappresenta l’acqua introdotta con la sabbia bagnata. Pertanto l’acqua introdotta con l’impiego degli inerti bagnati diventa:e questo quantitativo dovrà essere sottratto a quello previsto dal mix-design (200 kg/m³) con l’impiego di inerti in condizione di s.s.a.; l’acqua da introdurre come liquido in betoniera (a’) sarà pertanto 200 – 66 = 134 kg/m³.A seguito di questi calcoli, fondamentalmente basati sulle misure di umidità dei due inerti (3% e 6%) la composizione del calcestruzzo per rispettare le prestazioni previste dal mix-design diventa:

c = 300 kg/m³	=====>		=> a/c = 0,67 => R_ck = 25 MPa
a = 134 kg/m³
g = 1122 kg/m³		a = 200 => slump = 150 mm
s = 844 kg/m³

Come si può vedere la costanza di qualità, in termini di R_ck= 25 MPa e di slump = 150 mm, si può ottenere tenendo sotto costante controllo l’umidità degli inerti per apportare le necessarie modifiche nelle pesate di acqua, di sabbia e di ghiaia finalizzate al mantenimento effettivo nella quantità di a e di a/c, e quindi delle prestazioni.

Modifica delle pesate degli ingredienti rispetto al mix-design

Anche il diametro massimo e la granulometria dell’inerte possono influenzare la richiesta d’acqua (a) per ottenere una determinata lavorabilità. La correlazione tra diametro massimo e contenuto di acqua (a) per una determinata lavorabilità va sotto il nome di “regola di Lyse” (si consulti l’articolo “Acqua di impasto del calcestruzzo: fatti e misfatti sui cantieri” disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo) è così sintetizzabile: maggiore è il diametro massimo dell’aggregato, minore è la richiesta di acqua per una determinata lavorabilità. Ciò significa, ai fini della costanza di qualità, che la diminuzione del diametro massimo a seguito, per esempio, di un cambiamento nella fornitura di inerti deve comportare l’aumento nell’acqua di impasto (a) per tener costante la lavorabilità e conseguentemente, a pari a/c per tenere costante R_ck, un proporzionale aumento nel dosaggio di cemento (c).A parità di diametro massimo, la variazione di curva granulometrica può comportare una modifica nell’acqua (a) e quindi anche di c per mantenere costanti rispettivamente la lavorabilità e la resistenza meccanica.

Fig.3 – Variazione granulometrica nell’inerte.

Nella Fig.3 è mostrato schematicamente la variazione di granulometria rispetto alla curva A assunta come riferimento per la produzione costante di calcestruzzo. Se, per esempio a seguito dell’impiego di una sabbia più fine, la curva granulometrica diventa B, anziché A in Fig. 3, ci si può aspettare una maggiore richiesta d’acqua e quindi un maggior contenuto di cemento (a pari a/c) per mantenere costante la R_ck oltre allo slump. Per contro, l’adozione di una sabbia più grossa comporta una curva granulometria C, anziché A in Fig. 3: diminuirà allora la richiesta d’acqua (a) e si potrà anche ridurre il dosaggio di cemento (a pari a/c) per mantenere costanti slump ed R_ck purché non si manifestino fenomeni di segregazione e bleeding con conseguenze negative sulle caratteristiche di pompaggio e di getto (si consulti l’articolo “ Bleeding del calcestruzzo: acqua in superficie ma anche sotto” disponibile sul sito www.encosrl.it è l’ ABC del calcestruzzo).

Resistenza meccanica del calcestruzzo

Quale resistenza meccanica

La resistenza meccanica (R) è il massimo sforzo s che un materiale, in forma di una porzione geometricamente determinata (provino), è in grado di sopportare prima della rottura. A seconda che lo sforzo applicato sia a compressione (s_c), a flessione (s_f) o a trazione (s_t), si parlerà di resistenza meccanica a compressione (R_c), a flessione (R_f) o a trazione (R_t).Il calcestruzzo è un materiale che si comporta abbastanza bene sotto l’azione di uno sforzo a compressione, e mediocremente sotto quella di uno sforzo a trazione diretta o a trazione per flessione. Per questi ultimi tipi di sollecitazione, il calcestruzzo si affida al connubio con l’acciaio – notoriamente molto più resistente a trazione – in forma di armature metalliche per le strutture dette, appunto, in cemento armato (c.a.) che meglio sarebbe chiamare in calcestruzzo armato. Per questi motivi, ma anche per le difficoltà sperimentali insite nelle misure di R_t ed R_f, di solito sul calcestruzzo si effettuano solo misure dirette di R_c e si ricorre al calcolo per determinare indirettamente R_t, R_f ed anche E (modulo elastico).Val la pena di precisare che per il calcestruzzo è possibile misurare la resistenza meccanica a compressione su provini cubici (detti anche cubetti) ed in tal caso si adotta il simbolo R_c o su provini cilindrici (con rapporto altezza/diametro, h/D, di 2) ed in tal caso si adotta il simbolo f_c. Per uno stesso calcestruzzo, il valore di f_c è pari a circa l’80% di R_c:f_c = 0,80R_cLa differenza tra f_c ed R_c dipende sostanzialmente dal fatto che, nel sollecitare provini cilindrici “snelli” (cioè con un rapporto h/D=2), si instaura uno stato tensionale effettivo maggiore di quello che si registra per i provini cubici più “tozzi” (cioè con altezza eguale a larghezza).

**Resistenza Meccanica a compressione: il ruolo di a/c e** a

Attraverso la teoria di Powers è possibile calcolare la R_c di una pasta di cemento Portland in funzione del volume della porosità capillare (V_p) e del volume di cemento idratato (V_g), o del rapporto acqua-cemento (a/c) e del grado di idratazione (a), come è indicato nelle equazioni [2] e [4] dell’articolo che si trova sul sito www.encosrl.it è ABC del calcestruzzo: ”Porosità e permeabilità del calcestruzzo”:R_c= 250 [ 0,6790 ? / 0,3185 ? + (a/c )]³ [1]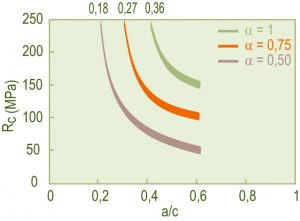

Fig. 1 – Influenza del rapporto a/c sulla resistenza meccanica a compressione (R_c) della pasta di cemento secondo Powers

Resistenza meccanica a compressione del calcestruzzo

Secondo l’equazione di Powers sopra riportata, la resistenza meccanica a compressione di una pasta di cemento dipende, a parità di temperatura, da a/c e da a (Fig. 1). Tuttavia, da un punto di vista pratico interessa di più la resistenza meccanica del calcestruzzo che è il vero materiale da costruzione. Inoltre, è difficile determinare il valore di a in un sistema più complesso come il calcestruzzo. D’altra parte a, in pratica, dipende dal tempo e dalla classe di resistenza del cemento. Pertanto i grafici della Fig. 2 che sono riferiti alla R_c del calcestruzzo in funzione di a/c vengono espressi in funzione del tempo di stagionatura (solitamente 1-3-7-28 giorni) e della classe di resistenza del cemento. Nella Fig. 2 vengono mostrati, a titolo di esempio la R_c per i calcestruzzi confezionati con cementi di classe 42.5R e 32.5R, misurati alle varie stagionature (da 1 a 28 giorni) alla temperatura di 20°C con U.R. ³ 95%.Le correlazioni R_c – a/c della Fig. 2 si riferiscono, come avviene in pratica per la misura di resistenza sui provini di calcestruzzo, a conglomerati sottoposti a compattazione a rifiuto, cioè con il massimo grado di compattazione possibile. Infatti, in assenza di questa precisa prescrizione, il risultato potrebbe essere influenzato, in modo significativo ma aleatorio, dal grado di compattazione, cioè dalla presenza di macrovuoti residui nel calcestruzzo per difetto di costipazione (aria intrappolata). In altre parole, due operatori che costipassero in modo diverso il calcestruzzo fresco otterrebbero risultati diversi nella resistenza meccanica e più bassi dove è minore il grado di compattazione cioè dove è maggiore il volume di aria intrappolata (si consulti l’articolo «”Lavorabilità del calcestruzzo fresco: influenza sul calcestruzzo in servizio» presente nel sito www.encosrl.it è l’ABC del calcestruzzo). Rimane il fatto, ovviamente, che la resistenza meccanica del calcestruzzo in opera potrà risultare tanto inferiore a quella del provino quanto minore è il grado di compattazione del calcestruzzo in opera rispetto a quella del calcestruzzo nel provino. Per ridurre questa differenza occorre impiegare calcestruzzi di maggior classe di consistenza (cioè più lavorabili) e quindi meno dipendenti dalla cura adottata nel compattare il calcestruzzo.Anche l’aria inglobata, cioè quella in forma di microbolle generate da un additivo aerante intenzionalmente aggiunto per produrre calcestruzzi resistenti al ghiaccio (si consulti l’articolo ”Gelo e disgelo del calcestruzzo” pubblicato sul sito www.encosrl.it è l’ABC del calcestruzzo), può provocare una diminuzione di resistenza meccanica che può essere prevista assumendo un calo di R_c di circa il 20% nel calcestruzzo con additivo aerante rispetto a quello privo di additivo aerante (Fig. 3): a parità di R_c richiesta (per es. 45 MPa) il rapporto a/c, che per un calcestruzzo senza aerante potrebbe essere 0,52, viene ridotto a 0,45 (Fig. 3) per compensare la caduta di resistenza provocata dalle microbolle di aria. In altre parole, non esiste alcun problema pratico nel prescrivere e produrre un calcestruzzo con una determinata R_c e resistente ai cicli di gelo-disgelo (e quindi con microbolle d’aria).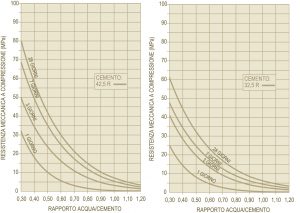

Fig. 2 – Resistenza a compressione in funzione del rapporto a/c alla stagionatura di 1 – 3 – 7 – 28 gg

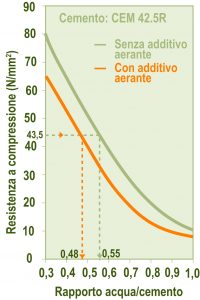
Fig. 3 – Resistenza a compressione a 28 gg per calcestruzzi confezionati con CEM 42.5R in assenza ed in presenza di additivo aerante (area = 4-6%)

Resistenza caratteristica R_ck

Con un DM del 1972 in ottemperanza alla legge N° 1086 sui calcestruzzi armati (c.a.) e precompressi (c.a.p.), fu introdotto in Italia il concetto di resistenza caratteristica (R_ck) in luogo di una generica resistenza a compressione mediata dai valori dei singoli prelievi tutti riferiti a 28 giorni: nR_cm28= ? R_ci28/n [2] 1Con l’avvento della legge N° 1086, occorre far riferimento non più alla R_cm28 ma ad una resistenza caratteristica (R_ck) più bassa, ottenuta penalizzando di un certo valore (kd) il valore di R_cm28:Dove R_ci28 è il valore di resistenza meccanica a compressione, a 28 giorni ottenuta nel prelievo iesimo (media di due provini), ed R_cm28è il valore medio a 28 giorni. Il valore di R_cm28 è riportato nei grafici della Fig. 2 sulle curve “28 giorni”.R_ck = R_cm28– kd [3]dove k è un valore fissato dal Ministero dei Lavori Pubblici (attualmente k vale 1.4), e d è lo scarto quadratico medio così calcolato: n_?= ? ( R_cm28 – R_ci28) / n – 1 [4] 1La differenza (R_cm28 – R_ci28) rappresenta lo scarto tra valor medio e valore individuale nel prelievo iesimo. In una produzione di calcestruzzo dove tutti i prelievi fossero tra loro coincidenti (e quindi anche eguali al valor medio) il valore di d nell’equazione [4] si annullerebbe ed il valore di R_ck calcolato con la [3] coinciderebbe con R_cm28: in altre parole non ci sarebbe alcuna penalizzazione; in realtà ? assume valori di circa 2-3 MPa in laboratorio (dove pure è possibile lavorare con buona riproducibilità di risultati da un impasto all’altro), di circa 3-4 MPa in una centrale di betonaggio che esercita un buon controllo di qualità, e di circa 5-7 MPa in una centrale produttiva da media a mediocre nel controllo della qualità.Appare evidente che quanto migliore è il controllo in fase produttiva, tanto minore è lo scarto quadratico medio d dell’equazione [4] e tanto minore è la penalizzazione kd nell’equazione [3] che occorre adottare per il calcolo della R_ck. In pratica, un produttore di calcestruzzo, fissata una certa R_ck in base al progetto strutturale dell’opera, e noto il valore di d della specifica centrale di betonaggio dove il calcestruzzo verrà prodotto, si pone come obiettivo il raggiungimento di una R_cm28 in grado di soddisfare la disequazione [5]:R_cm28 ³ R_ck+kd [5]In altre parole se il valore di d su un impianto produttivo è di 5 MPa, a fronte di una richiesta del progettista di R_ck = 25 MPa occorre garantire almeno una R_cm28 di 25 + 1,4 · 5 = 32 MPa. Ovviamente valori maggiori di 32 MPa per R_cm28 soddisfano ancor meglio la disequazione [5].A maggior garanzia della sicurezza dell’opera è richiesto che il minimo valore di resistenza meccanica (R_cmin28) tra tutti i singoli prelievi (R_ci28) debba soddisfare la disequazioneR_{c min28} ³ R_ck– 3,5MPa [6]Ciò significa che per un dato valore di R_ck (per es. 25 MPa) nessun prelievo dovrà risultare meno di 21.5 MPa in base alla disequazione [6]. Se ciò dovesse avvenire (per es. R_cmin28 = 16.5 MPa) la R_ck dovrà essere declassata da 25 MPa a 20 MPa per soddisfare oltre alla disequazione [5] anche la disequazione [6]. Ciò comporterà ovviamente che, a fronte di una R_ck più bassa (20 contro 25 MPa) il progettista si esprimerà sulla opportunità o meno di provvedere a lavori supplementari sull’opera per compensare la riduzione di R_ck o addirittura di abbattere la struttura in caso di gravi deficienze strutturali per la minor classe di resistenza del calcestruzzo.Le due disequazioni [5] e [6] sono raccomandabili per lavori molto importanti soprattutto se di grande impegno volumetrico (>1500 m³). Il tipo di controllo basato sulle disequazioni [5] e [6] è chiamato controllo di tipo B. Esiste un controllo di tipo A, dove seguita a valere la disequazione [6] per assicurare che non ci siano valori individuali più bassi di 3,5 MPa rispetto alla R_ck. Nel controllo di tipo A, la R_ck viene calcolata con la disequazione[7] anziché con la [5]:R_cm28 ³ R_ck+ 3,5MPa [7]In altre parole si assume “forfettariamente” un valore kd pari a 3.5 MPa purché si assicuri, però, che nessun prelievo (R_cmin28) scenda al di sotto della R_ck per più di 3.5 MPa come prescritto dalla [6].

Resistenza meccanica a flessione ed a trazione

La resistenza meccanica a flessione ed a trazione dipendono, oltre che dal rapporto a/c e dal grado di idratazione (quindi dal tempo e dalla classe di resistenza del cemento), anche dal tipo di inerte che gioca invece un ruolo meno importante nella resistenza a compressione. Nella Fig. 4 è mostrato, esemplificativamente per il cemento CEM 32.5 ed il tempo di 28 giorni, la dipendenza di R_f (valore medio) in funzione di a/c per calcestruzzi confezionati con inerte alluvionale (tondeggiante e liscio) o con inerte di frantumazione (irregolare e ruvido).Come si può notare, la Fig. 4 mostra due distinte curve di correlazione R_f – a/c a seconda dell’inerte impiegato, mentre nella Fig. 5 è mostrata un’unica curva di correlazione tra R_cm28 ed a/c indipendentemente dall’inerte impiegato. Si può osservare che, a parità di a/c, il calcestruzzo presenta una maggiore R_fse l’inerte è di forma irregolare e di tessitura ruvida (cioè frantumato). Infatti, rispetto all’inerte alluvionale di forma tondeggiante e tessitura liscia, si realizza un miglior giunto adesivo all’interfaccia inerte frantumato–pasta cementizia. Questo legame influenza molto più R_f (ed anche R_t) che non R_c per le sollecitazioni di trazione che si generano proprio all’interfaccia inerte-pasta durante le sollecitazioni di s_f e s_t.Si consideri ora una pavimentazione in calcestruzzo per la quale, accanto ad una R_ck di 30 MPa (controllo di tipo A), si richiede a 28 giorni una R_f di 6 MPa e sia disponibile un inerte frantumato. Dalla Fig. 4 si ricava che, per realizzare l’obiettivo della R_f, occorre adottare un a/c di 0,40. D’altra parte alla R_ck di 30 MPa corrisponde (con il controllo di tipo A, secondo la disequazione [6]) una R_cm28 di 33,5 MPa e quindi sarebbe sufficiente adottare un a/c di 0,59 in base al grafico di Fig. 5 (seguire il percorso della freccia dall’asse di R_cm28, 33,5 MPa quello di a/c). Ci si trova, in sostanza, davanti ad una richiesta “incongruente” giacché le due esigenze prestazionali R_ck ed R_f (a 28 giorni) portano a due diversi valori di a/c (rispettivamente di 0,59 e 0,40), mentre per confezionare il calcestruzzo occorre ovviamente adottare un a/c (ed uno solo). Per risolvere l’incongruenza, e soddisfare entrambe le prestazioni richieste, esiste un solo modo: quello di adottare il più basso tra i due valori di a/c e cioè, in questo esempio, 0,40 determinato dalla R_f. E’ ovvio che adottando per a/c il valore di 0,40, la R_cm28 (seguire in Fig. 5 il percorso della freccia dal basso verso l’alto) risulterà più elevata di quella richiesta per soddisfare l’originale valore di R_ck (30 MPa). In altre parole, per soddisfare la R_f e quindi adottare per a/c il valore di 0,40, la effettiva resistenza caratteristica (indicata con R_ck* per distinguerla da quella nominale R_ck) risulterà essere:R*_ck = 57-3,5 = 53,5MPa [8]

dove 57 MPa rappresenta la R_cm28 in Fig. 5 con il rapporto a/c di 0,40. Poiché il costo del calcestruzzo è solitamente basato sulla resistenza caratteristica, il calcolo sopra illustrato consente anche di valutare obiettivamente il valore economico del calcestruzzo in base all’effettiva resistenza caratteristica (R*_ck), determinata dalla R_f = 6 MPa, piuttosto che in base a quella nominale (R_ck).

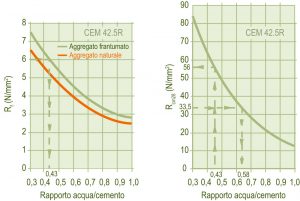
Fig. 4 – Influenza del rapporto a/c sulla resistenza a flessione a 28 giorni (R_f) con aggregati naturali e frantumati

Fig. 5 – Influenza del rapporto a/c sulla resistenza a compressione a 28 giorni (R_cm28) indipendentemente dalla qualità dell’aggregato (naturale o frantumato).

Correlazione tra R_c ed R_f o R_t

Per calcolare facilmente il passaggio dal valore di R_f al corrispondente valore di R_cm, senza ricorrere all’ausilio di grafici (come quelli mostrati per il CEM 32.5 in Fig. 4) in genere difficilmente disponibili per tutti i cementi, si può impiegare l’equazione [9]:R_t = K_t · ?Rc [9]dove k_f è una costante che vale 0,7 per inerti alluvionali e 0,8 per quelli di frantumazione. La resistenza a trazione diretta R_t può essere, a sua volta, calcolata dalla R_f attraverso l’equazione [10]:R_t = K_t · R_f[10]dove k_t è una costante che vale 0.6 per calcestruzzo con R_cm > 20 MPa e 0.5 per quelli con R_cm < 20 MPa.

Correlazione tra R_c ed E

Per completare il quadro delle correlazioni, si può menzionare quella tra R_c(o R_ck) ed il corrispondente modulo elastico E: la correlazione è sempre del tipo E = Ke · ?Rc [11]dove il valore della costante K_E dipende dalle unità di misura adottate, da come è misurata la resistenza meccanica a compressione (R_c per provini cubici o f_c per quelli cilindrici) ed E (modulo elastico tangenziale iniziale o modulo elastico secante).Per la normativa italiana, in assenza di misure dirette per E, il modulo elastico può essere calcolato con l’equazione [12]:E28 = 5850 · ?R_ck[12]dove E₂₈ ed R_ck sono misurati a 28 giorni in MPa, R_ck è riferito a provini cubici, ed E₂₈ è il modulo elastico secante cioè ?_1/3/?_1/3 dove ?_1/3 è la deformazione unitaria che corrisponde all’applicazione di uno sforzo (?_1/3) pari ad 1/3 della resistenza meccanica a compressione (R_c28).In realtà l’equazione [12], o altre equivalenti all’equazione [11] con diversi valori di K_E, sono delle correlazioni molto approssimate e non tengono conto del fatto che il modulo elastico dipende non solo dalla resistenza meccanica (cioè, in definitiva dal valore di a/c e dalla classe del cemento prescelto) ma anche dalla proporzione tra il componente più rigido (l’inerte generalmente con E molto elevato) e quello più deformabile (pasta di cemento con E molto minore) come è mostrato in Fig. 6. Il modulo elastico del calcestruzzo (E) dipende dalla pendenza iniziale della curva ?-? della Fig. 6: quanto maggiore è il contenuto di inerte nel calcestruzzo, tanto più la curva ?-? del calcestruzzo si avvicinerà a quella dell’inerte. D’altra parte, in un conglomerato ricco di cemento e povero di inerte (per es. una malta) la curva ?-? del conglomerato sarà più vicina alla curva ?-? della pasta cementizia.Occorre inoltre tener conto che, sia per l’inerte sia per la pasta di cemento, il modulo elastico, rispettivamente E_i ed E_p, sarà dipendente dal tipo di roccia più o meno rigida (granito, basalto, calcare, quarzite) o dal tipo di pasta cementizia (maggiore è a/c, minore è E_p).Per l’effettivo calcolo di E del calcestruzzo occorrerebbe far riferimento, più che alle equazioni [11] e [12], alle equazioni [13] e [14] dove E viene espresso in funzione dei moduli elastici E_i dell’inerte (circa 70-90 GPa), ed E_p della pasta di cemento (circa 20-30 GPa), oltre che delle loro rispettive frazioni volumetriche v_i e v_p:E = v_i· E_i + v_p· Ep = v_i· E_i + ( 1 – v_i ) · Ep [13] 1/ E = v_i· ( 1/E_i) + v_p· ( 1/Ep ) = ( v_{i /} E_i) + ( 1 – v_i / Ep ) [14]L’equazione [13] si basa sulla teoria dei materiali compositi dove i componenti inerte e pasta di cemento sono sottoposti allo stesso sforzo ?, mentre l’equazione [14] è riferita al modello che assume una stessa deformazione ? per i due componenti. In pratica, il modulo elastico del calcestruzzo potrà variare entro un intervallo di valori calcolabili con le equazioni [13] e [14] purché siano noti i valori di v_i, E_i ed E_p. Poiché quasi sempre E_i >E_p l’aumento del modulo elastico del calcestruzzo E si realizza in pratica aumentando il volume di inerte (scegliendo un diametro massimo il più elevato possibile) e/o, sia pure in subordine, riducendo il rapporto a/c della matrice cementizia.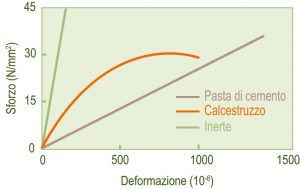

Fig. 6 – Tipico comportamento sforzo-deformazione del calcestruzzo e dei suoi componenti (inerti e pasta cementizia)

Superfluidificanti ed altri additivi per il calcestruzzo

Gli additivi

I superfluidificanti appartengono alla categoria degli additivi per calcestruzzo (M. Collepardi and V.S.Ramachandran, “Effect of Admixtures”, 9th International Congress on the Chemistry of Cement”, pp. 529-570, New Delhy, India, 23-28 November ,1992), cioè di quei prodotti chimici aggiunti, solitamente in piccole quantità, agli altri ingredienti del calcestruzzo al fine di migliorarne una o più prestazioni. A seconda della funzione coinvolta nel miglioramento gli additivi possono essere classificati in vari tipi, i più importanti dei quali sono:- acceleranti- ritardanti- superfluidificanti (e fluidificanti)- aerantiGli additivi acceleranti e quelli ritardanti hanno la funzione di modificare il grado di idratazione (a) del cemento solo alle brevi stagionature e modificano, quindi, le prestazioni del calcestruzzo in corso di esecuzione ma non le prestazioni delle strutture in esercizio. Gli additivi acceleranti, in particolare, fanno aumentare il grado di idratazione del cemento alle brevi stagionature in modo da accorciare i tempi di presa (acceleranti di presa) o di incrementare la resistenza meccanica nei primi giorni (acceleranti di indurimento) sopra tutto nei climi invernali quando la bassa temperatura rallenta il decorso della reazione iniziale tra l’acqua ed il cemento. L’effetto accelerante serve, per esempio, all’impresa per stagionare e rifinire più in fretta un pavimento in calcestruzzo che presenta tempi di presa troppo lunghi, o per scasserare più in fretta i getti di calcestruzzo senza immobilizzare troppo a lungo le casseforme. Gli acceleranti non modificano la resistenza meccanica del calcestruzzo alle lunghe stagionature, cioè in servizio, e pertanto le prestazioni delle strutture in opera non risentono beneficamente della eventuale presenza di acceleranti. Anzi, in passato, quando si impiegavano acceleranti a base di cloruri si sono registrati fenomeni di corrosione delle armature quando si eccedeva nel dosaggio di questi additivi.Gli additivi ritardanti, invece, hanno la funzione di ridurre il grado di idratazione (a) del cemento nelle prime ore, soprattutto in climi caldi quando l’alta temperatura accelera l’idratazione del cemento ostacolando il trasporto del calcestruzzo (perdita di lavorabilità), le operazioni di getto e quelle di finitura. Anche questi additivi aiutano l’impresa a risolvere qualche problema in fase esecutiva ma non modificano sostanzialmente le prestazioni del materiale in servizio.Gli additivi aeranti (Air-Entraining Agents, AEA, in inglese), invece, modificano le prestazioni del calcestruzzo in servizio migliorandone la resistenza al ghiaccio (si consulti l’articolo “Gelo e disgelo del calcestruzzo” presente nel sito www.encosrl.it è l’ABC del calcestruzzo).Gli additivi superfluidificanti ed in minor misura gli additivi fluidificanti modificano – a seconda del loro impiego – le prestazioni del calcestruzzo in corso di esecuzione e/o quelle in esercizio (durabilità, resistenza meccanica, ritiro, ecc.).

L’avvento dei superfluidificanti

Agli inizi degli anni 1970, la famiglia dei fluidificanti (a base di ligninsolfonato, un residuo dell’estrazione della cellulosa dal legno) fu tecnicamente sovrastata da superfluidificanti prodotti per sintesi chimica. In sostanza si potrebbe dire che le prestazioni di questi ultimi, nel seguito descritte, sono circa quattro volte più efficaci rispetto a quelle dei fluidificanti.Tutti i superfluidificanti sono basati su polimeri idrosolubili. I primi ad essere immessi sul mercato erano basati su poli-naftalin-solfonato (PNS) o su poli-melammin-solfonati (PMS). Più recentemente verso la fine del 1980 sono stati introdotti i poli-acrilati (PA) o poli-carbossilati (PC) che formano una famiglia molto vasta di nuovi polimeri tutti caratterizzati dall’assenza dei gruppi solfonici presenti nei PNS e PMS. Nella Fig. 1 sono mostrate le molecole di questi superfluidificanti.In linea di massima la quantità di additivo impiegata, rispetto alla massa del cemento, si aggira sull’1%. Ovviamente diminuendo o aumentando l’additivo (di solito non oltre il 2%) si riduce o si incrementa l’effetto dell’additivo.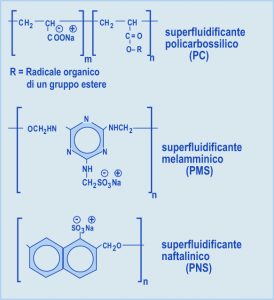Fig. 1 – Composizione chimica dei più importanti superfluidificanti

Le “tre facce di una stessa medaglia”

A seconda del modo di impiego, il calcestruzzo con superfluidificante può presentare rispetto al corrispondente calcestruzzo privo di additivo, determinati miglioramenti prestazionali. I possibili modi di impiego sono tre: essi tra loro strettamente correlati e tutti dipendenti da un unico effetto dell’additivo sul sistema acqua-cemento. Si potrebbe dire che si tratta delle “tre facce della stessa medaglia“.La “medaglia” è l’effetto deflocculante dell’additivo sui granuli di cemento dispersi in un mezzo acquoso. Una miscela di cemento molto diluita in acqua, depositata su vetro trasparente illuminato dal basso in alto con una lampada, osservata con microscopio ottico si presenta come nella foto della Fig. 2A: i granuli di cemento, opachi alla luce, si presentano come macchie nere mentre la parte bianca della foto corrisponde alla presenza dell’acqua che è trasparente alla luce. Salvo pochissimi granuli, che corrispondono alle macchie puntiformi nere, la maggior parte dei granuli di cemento si presenta in forma di agglomerati di molti granuli di cemento. Questo fenomeno – noto come flocculazione – deriva dall’attrazione di natura elettrostatica tra i vari granuli di cemento a seguito delle cariche elettrostatiche di segno opposto che si sono formate sulle superfici dei granuli per effetto della macinazione (e della rottura dei legami ionici presenti nei costituenti del clinker) durante il processo produttivo del cemento.In presenza dei superfluidificanti, i diversi granuli sono deflocculati, cioè dispersi (Fig. 2B) a seguito di uno dei due possibili meccanismi (A. Borsoi, S. Collepardi L. Coppola, R. Troli e M. Collepardi, “Progressi nei superfluidificanti per calcestruzzi”, L’Industria Italiana del Cemento, N° 741, pp 234-245, 1999):- adsorbimento sulla superficie dei granuli di cemento delle molecole di superfluidificante e formazione di cariche elettrostatiche dello stesso segno (negative) apportate dai gruppo anionici dei superfluidificanti PNS e PMS che provoca una repulsione elettrostatica (zeta potential) tra i granuli di cemento;- adsorbimento sulla superficie dei granuli di cemento delle molecole di superfluidificante PA che grazie alla ingombrante presenza delle catene laterali, impedisce ai granuli di cemento di avvicinarsi (steric hindrance) e di flocculare.Indipendentemente dal particolare meccanismo di azione (zeta potential o steric hindrance), l’effetto deflocculante dei superfluidificanti, nei confronti degli agglomerati formati da numerosi granuli di cemento (Fig. 2), può essere utilizzato in tre modi diversi (“tre facce”):- a pari composizione del calcestruzzo- con riduzione di acqua e di a/c (a pari cemento e lavorabilità)- con riduzione di acqua e cemento (a pari a/c e lavorabilità)

Fig. 2 – Osservazione al microscopio ottico di una pasta di cemento flocculata (A) e dispersa (B) per la presenza di additivo superfluidificante

Aggiunta del superfluidificante a pari composizione del calcestruzzo

Questa modalità di impiego consiste nell’aggiungere l’additivo ad una miscela cementizia (pasta, malta o calcestruzzo) senza alcuna modifica nella composizione ed in particolare del rapporto acqua-cemento (a/c). L’effetto è immediatamente visibile e consiste nell’aumento della fluidità della pasta (Fig. 3) o del calcestruzzo (Fig. 4). L’aumento di fluidità, conseguibile senza modifica del rapporto a/c, è strettamente correlabile con l’effetto disperdente (Fig. 2) giacché i granuli di cemento “individuali” – come sono nel sistema deflocculato di Fig. 2B – si muovono molto più liberamente e velocemente rispetto ai granuli del sistema flocculato (Fig. 2A) che si muove con più difficoltà a causa del suo maggior ingombro.La Fig. 5 illustra esemplificativamente le variazioni di prestazioni nella trasformazione di un calcestruzzo a consistenza S1 (terra umida) in un calcestruzzo a consistenza superfluida S5 (slump ³ 21 cm) a seguito dell’aggiunta di un superfluidificante (1% sul cemento) come mostrato in Fig. 4. A dire il vero nel passare da S1 ad S5 conviene aumentare il rapporto sabbia/ghiaia per ridurre la segregazione. Il vantaggio nell’impiegare l’additivo con queste modalità (cioè per migliorare la lavorabilità) comporta una maggiore affidabilità del getto della struttura reale che presenterà un maggior grado di compattazione indipendentemente dalla costipazione e dalla qualità della manodopera (si consulti l’articolo .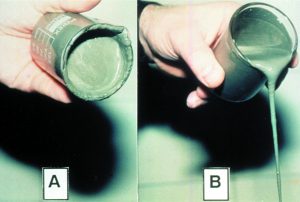

Fig. 3 – Pasta di cemento con rapporto a/c=0.35 in assenza (A) ed in presenza (B) di additivo superfluidificante

Fig. 4 – Calcestruzzo con rapporto a/C=0.45 in presenza ed in assenza di additivo superfluidificante

Fig. 5 – Aggiunta del superfluidificante (1%) senza modifica nella composizione del calcestruzzo (in particolare a pari a/c) e senza modifica delle prestazioni del calcestruzzo indurito

Aggiunta del superfluidificante a pari lavorabilità con riduzione di acqua e di a/c

Nell’esempio precedente (Fig. 5) si è mostrato il comportamento dell’additivo da vero e proprio superfluidificante perché fa aumentare la fluidità del sistema. Verrà ora illustrato l’esempio di impiego dell’additivo in forma di “super-riduttore di acqua” più che di superfluidificante vero e proprio. In realtà, come si è già detto, si tratta di una diversa (seconda) “faccia della stessa medaglia”: se è vero che il superfluidificante fa aumentare la classe di consistenza (nel caso di Fig. 5 da S1 ad S5), si può immaginare di aggiungere l’additivo e contemporaneamente di ridurre l’acqua di impasto (a) in modo da lasciare immutata la lavorabilità: in sostanza si approfitta del potere fluidificante dell’additivo per ridurre l’acqua di impasto a pari lavorabilità.In linea di massima, con un dosaggio dell’1% di additivo si può ridurre l’acqua del 15 o 20% (con PNS e PMS o con PA rispettivamente). Se ci si limita a ridurre l’acqua senza modificare il dosaggio di cemento (e compensando il volume di acqua ridotto con un eguale aumento del volume di inerte), il risultato finale sarà una diminuzione del 15-20% nel rapporto a/c a pari lavorabilità del calcestruzzo come è esemplificato in Fig. 6.A seguito della riduzione nel rapporto a/c si registra- una minore porosità e permeabilità;- una migliore durabilità- una maggiore resistenza meccanica;

Fig. 6 – Aggiunta del superfluidificante (1%) con riduzione di acqua (-20%) e del rapporto a/c (-20%), a pari lavorabilità, con miglioramento della durabilità ed aumento della resistenza meccanica

Aggiunta del superfluidificante a pari lavorabilità ed a/c con riduzione di acqua e cemento

La “terza” faccia della stessa medaglia è in realtà una combinazione delle due precedenti ed è sempre correlata con l’effetto disperdente-deflocculante dei granuli di cemento da parte del superfluidificante (Fig. 2).Supponiamo, per esempio, di partire da un calcestruzzo senza additivo già a consistenza superfluida (S5) per il quantitativo elevato di acqua (a = 220 Kg/m³), già meccanicamente resistente (R_ck= 45 MPa) per il basso a/c (0.45), oltre che durabile e impermeabile. In conseguenza dell’elevato quantitativo di acqua (220 Kg/m³) e del basso rapporto a/c (0.45) il dosaggio di cemento diventa relativamente elevato :c = a/(a/c) = 220/0,45 = 489 kg/m3Inoltre, l’elevato contenuto di cemento comporta un forte sviluppo di calore con rischi di fessurazioni per l’insorgere di rilevanti gradienti termici ed elevata deformazione viscosa.L’elevato quantitativo di acqua per aumentare la lavorabilità e l’elevato dosaggio di cemento (c), che consegue da un alto valore di a ed un basso valore di a/c, comporta anche un ridotto quantitativo di inerte (i), ed un basso rapporto inerte-cemento (i/c) con elevata tendenza al ritiro igrometrico.Nella Fig. 7 è schematicamente mostrata la variazione di composizione (a pari a/c, R_ck e lavorabilità) con aggiunta di superfluidificante (1%) per aumentare i/c (e ridurre quindi il ritiro igrometrico), e per ridurre c (e diminuire quindi lo sviluppo di calore ed il gradiente termico, oltre che la deformazione viscosa).

Fig. 7 – Aggiunta del superfluidificante (1%) con riduzione di acqua (-20%) e di cemento (-20%), a pari lavorabilità, resistenza meccanica e durabilità, con riduzione di ritiro igrometrico, gradiente termico e deformazione viscosa

Conclusioni

L’impiego dei superfluidificanti ha rivoluzionato il mondo delle costruzioni in c.a. e c.a.p.. E’ possibile, infatti, a seconda della modalità di impiego:- migliorare la lavorabilità e l’affidabilità delle strutture in opera (a pari a/c);- aumentare R_ck e durabilità riducendo l’acqua (a) e quindi a/c (a pari lavorabilità);- ridurre il ritiro igrometrico, il gradente termico e la deformazione viscosa riducendo sia l’acqua (a) che il cemento (c), a pari a/c e pari lavorabilità.

Temperatura del calcestruzzo

La temperaturaLa temperatura gioca un ruolo considerevole sulle prestazioni meccaniche del calcestruzzo (in particolare, sul loro decorso in funzione del tempo di stagionatura), e sul comportamento del calcestruzzo in servizio dal punto di vista della durabilità oltre che della resistenza meccanica. Nei paragrafi che seguono verranno esaminati i seguenti argomenti:- influenza della temperatura sulla resistenza meccanica;- influenza della temperatura sull’organizzazione del cantiere;- trattamenti termici a vapore;- calore di idratazione, gradienti termici e rischi di fessurazione.

Influenza della temperatura sulle prestazioni meccaniche

Le prove di norma (EN 197/1) che vengono eseguite sulle malte per la classificazione meccanica dei cementi e quelle (EN 206) per la determinazione della R_ck dei calcestruzzi, debbono essere entrambe eseguite su materiali stagionati in condizioni termo-igrometriche standard ed in particolare a 20°C. La scelta di una ben determinata temperatura deriva proprio dal fatto che essa influenza il risultato della resistenza meccanica tanto dei cementi (in forma di malta) quanto dei calcestruzzi. Poiché a questa prestazione meccanica viene correlato il costo di questi materiali, è necessario, per stabilire regole chiare e certe tra fornitore e committente, precisare una temperatura di riferimento (appunto 20° C) alla quale stagionare malte e calcestruzzi prima di determinarne la resistenza meccanica.I calcestruzzi, però, nella pratica di cantiere sono gettati e stagionati a temperature talvolta molto diverse dai 20°C. E’ importante, quindi, conoscere la correlazione tra temperatura di stagionatura e resistenza meccanica del calcestruzzo per poter prevedere, sulle basi dei risultati a 20°C, le prestazioni dei calcestruzzi in cantiere a qualsiasi temperatura ambientale.La Fig. 1 mostra, esemplificativamente, la resistenza meccanica a compressione R_c dello stesso calcestruzzo stagionato a 10°C, 20°C e 30°C fino a 90 giorni. Dall’esame dei risultati illustrati in Fig. 1 si possono fare tre considerazioni pratiche:

alle brevi stagionature (1-7 gg) maggiore è la temperatura, maggiore è la resistenza meccanica a compressione;
alle lunghe stagionature (>> 28 gg) minore è la temperatura, maggiore è la resistenza meccanica a compressione;
a 28 giorni le resistenze meccaniche a compressione alle temperature ambientali fredde (10°C) o calde (30°C) non sono molto diverse da quelle alla temperatura standard di riferimento (20°C).

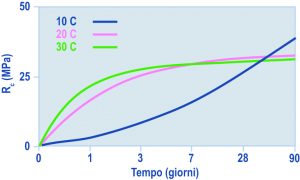Fig. 1 – Decorso della resistenza meccanica a compressione (R_c) di un calcestruzzo in funzione del tempo a diverse temperatureIn base alla considerazione 1) un clima invernale riduce la resistenza meccanica alle brevi stagionature e ciò dipende dal fatto che la reazione di idratazione del cemento procede più lentamente alle basse temperature. In altre parole R_cè minore alle basse temperature perché è minore il grado di idratazione a. In base alla considerazione 2), un clima invernale fa aumentare la resistenza meccanica alle lunghe o lunghissime stagionature, ma questo aumento difficilmente può essere correlato con il grado di idratazione; infatti, è presumibile che, a qualsiasi stagionatura, aumenti con la temperatura come avviene solitamente per ogni processo chimico (Fig. 2). L’aumento di R_c al diminuire della temperatura alle lunghe stagionature (Fig. 1), nonostante che a non aumenti al diminuire della temperatura (Fig. 2), porta a ritenere che la qualità delle fibre del C-S-H sia responsabile di questo effetto. In altre parole, la qualità delle fibre che crescono lentamente a bassa temperatura è migliore (cioè sono meccanicamente più “robuste”) di quelle che crescono velocemente ad alta temperatura; tuttavia, alle brevi stagionature prevale la maggiore quantità delle fibre di C-S-H (cioè il valore più alto di ?) sulla loro inferiore qualità nel determinare una crescita di R_c con la temperatura; alle lunghe ed ancor più alle lunghissime stagionature, quando il valore di ? si approssima ad 1 anche alle basse temperature (Fig. 2) (cioè quando la quantità di fibre di C-S-H è più o meno la stessa alle diverse temperature), allora la migliore qualità delle fibre di C-S-H, che si formano a bassa temperatura, prevale nel determinare la resistenza meccanica. La considerazione 3) giustifica perché la R_ck sia convenzionalmente misurata in laboratorio a 20°C dopo 28 giorni, quando cioè non cambia significativamente con la temperatura: pertanto la resistenza meccanica misurata in laboratorio a 20°C non è molto diversa da quella eventualmente misurata alle temperature del cantiere.La Fig. 1 mostra che alle basse temperature (0-5°C), quando la reazione di idratazione del cemento procede lentamente, occorrono tempi lunghi per raggiungere e superare le prestazioni ottenute alle temperature più elevate. In altre parole i calcestruzzi gettati e maturati in inverno, presentano in servizio le prestazioni migliori. E allora perché le imprese preferiscono l’estate all’inverno per l’esecuzione delle opere in calcestruzzo? La ragione di questa scelta è legata alla produttività del processo costruttivo piuttosto che alla qualità della costruzione in servizio come è mostrato nel prossimo paragrafo.

Influenza della temperatura ambientale sul getto in cantiere

Nel periodo invernale gli inconvenienti principali sono legati al ritardo iniziale nella presa e nell’indurimento. Questo ritardo provoca un allungamento dei tempi di finitura nei pavimenti e negli intonaci, ed un rinvio nella scasseratura delle strutture che richiedono un raggiungimento di 5-10 MPa nella R_c. Per evitare questi inconvenienti è consigliabile:- evitare i getti nel tardo pomeriggio con inevitabile raffreddamento notturno che coincide con le prime ore di stagionatura;- proteggere, se possibile, gli ingredienti (soprattutto gli inerti) dal freddo e soprattutto dal gelo;- proteggere i getti non casserati (pavimenti) con teli o isolamenti termici (pannelli in polistirolo) per non disperdere il calore di idratazione che favorisce un aumento di temperatura nel calcestruzzo rispetto all’ambiente;- impiegare preferibilmente cementi di classe 35.5R invece che 32.5 o, ancor meglio, di classe 42.5R;- impiegare, se possibile, acqua calda per l’impasto da mescolare con gli inerti prima dell’aggiunta del cemento;- impiegare additivi acceleranti e riduttori di acqua non ritardanti per incrementare la R_c alle brevi stagionature;- rinviare il getto a giorni con clima meno sfavorevole quando la temperatura è prossima a 0°C, quando cioè lo sviluppo della R_c è fortemente rallentata e soprattutto quando esiste un rischio di danno irreversibile nel calcestruzzo ancora “tenero” per una gelata che fa congelare l’acqua libera dell’impasto cementizio.Nel periodo estivo, invece, il maggior problema è rappresentato dalla perdita di lavorabilità del calcestruzzo fresco a causa dell’accelerazione del processo d’idratazione alle brevissime stagionature con l’aumento di temperatura (Fig. 2). Per ovviare a questo inconveniente – che spesso si traduce in ri-aggiunte d’acqua sul cantiere- si può raffreddare il calcestruzzo aggiungendo ghiaccio tritato in luogo di acqua normale o, più semplicemente, utilizzando additivi ritardanti o superfluidificanti di tipo ritardante.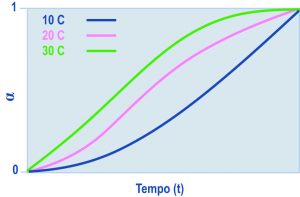Fig. 2 – Influenza della temperatura sul decorso del grado di idratazione (a)

Trattamento termico del calcestruzzo in prefabbricazione

Il trattamento termico consiste nel riscaldare artificialmente il calcestruzzo al fine di accelerare l’idratazione del cemento e di ottenere, quindi, in tempi brevi (qualche giorno) una prestazione solitamente ottenibile in cantiere nel giro di qualche settimana.L’esigenza del riscaldamento del calcestruzzo nasce soprattutto nei Paesi Nordici dove, per un lungo periodo dell’anno le condizioni climatiche sono sfavorevoli, per le basse temperature, ad un normale indurimento del calcestruzzo. Questa tecnica consente, proprio grazie alla maturazione accelerata, di ottenere rapidamente elementi strutturali (travi, pilastri, pannelli, lastre, ecc) prodotti in un impianto industriale (prefabbricazione) da trasportare e montare in cantiere. Successivamente, proprio per i vantaggi conseguibili con un’elevata produttività, il trattamento termico è stato adottato anche in Paesi, come il nostro, dove le condizioni climatiche sfavorevoli al getto del calcestruzzo nei cantieri sono limitate a pochi giorni o al massimo a 1-2 mesi. Tuttavia l’adozione della maturazione accelerata si giustifica economicamente quando il numero di elementi prefabbricati da produrre è elevato e conseguibile solo con una determinata cassaforma.Il riscaldamento deve avvenire senza che il calcestruzzo perda parte della sua acqua di impasto con conseguenti rischi di fessurazione promossa dal ritiro. Per evitare il rischio di fessurazione occorre realizzare il riscaldamento in un ambiente sempre saturo di vapore.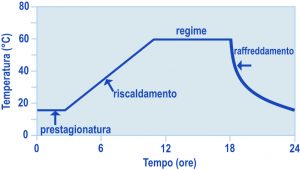Fig. 3 – Diagramma temperatura-tempo per un trattamento termico in prefabbricazioneLa Fig. 3 mostra un tipico diagramma temperatura-tempo (T – t) nel quale si possono individuare quattro stadi:- stagionatura preliminare (pre-stagionatura) a temperatura ambiente;– riscaldamento da temperatura ambiente a quella di regime:- conservazione della temperatura a regime;– raffreddamento della temperatura di regime a quella ambientale.E’ necessario rispettare alcune regole pratiche per evitare fessurazioni degli elementi prefabbricati (con grave pregiudizio per la loro durabilità) a causa di gradienti termici tra i vari ingredienti del calcestruzzo:

la pre-stagionatura deve essere almeno di 2 ore in modo che il calcestruzzo, all’inizio del riscaldamento, non sia ancora fluido e presenti invece un minimo di consistenza (slump £ 1 cm); il tempo di pre-stagionatura si riduce all’aumentare della classe di resistenza del cemento e della temperatura ambientale; in caso di calcestruzzo resistente al gelo, e quindi con microbolle d’aria, è necessario ancor più evitare di esporre il calcestruzzo fresco al riscaldamento quando è ancora troppo fluido per limitare un indesiderato rigonfiamento del calcestruzzo per la dilatazione termica delle microbolle d’aria;
la velocità di riscaldamento (T/dt) deve essere compresa tra 10 e 30 °C/ora, preferibilmente non superiore a 20°C/ora, soprattutto se non si può rispettare il vincolo della pre-stagionatura (t ³ 2 ore); con una pre-stagionatura di almeno 2 ore e con una velocità di riscaldamento non superiore a 20°C/ora le strutture dovrebbero risultare integre al termine del ciclo di vapore, mentre il rischio di fessurazione aumenta riducendo la pre-stagionatura e/o aumentando la velocità di riscaldamento oltre i limiti sopra menzionati;
è consigliabile adottare una temperatura di regime non eccessivamente elevata, preferibilmente non superiore a 60°C, per evitare rischi di fessurazione postuma da DEF;
è necessario evitare uno shock termico in fase di raffreddamento, soprattutto scasserando gli elementi prefabbricati ancora caldi in clima invernale, per non innescare fessure di origine termica.

In Fig. 4 è mostrato un tipico sviluppo di resistenza meccanica a compressione per lo stesso calcestruzzo stagionato sempre a temperatura ambiente (20°C) o maturato a vapore (con il ciclo termico della Fig. 3) e quindi stagionato a temperatura ambiente. Alle brevi stagionature (1-3 giorni) la R_c è maggiore nel calcestruzzo trattato a vapore; a 7 giorni le resistenze meccaniche con e senza trattamento termico si equivalgono; alle stagionature più lunghe la R_c è maggiore nel calcestruzzo stagionato naturalmente che non in quello trattato a vapore e la differenza può essere ascritta alla qualità delle fibre di C-S-H come già illustrato precedentemente.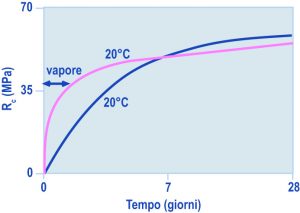Fig. 4 – Influenza del trattamento a vapore sulla resistenza meccanica a compressione (R_c) rispetto a quella dello stesso calcestruzzo stagionato sempre a 20°C

Calore di idratazione, gradienti termici e rischi di fessurazione

L’idratazione del cemento è una reazione esotermica che avviene con sviluppo di calore. Il calore di idratazione unitario, cioè riferito ad 1 Kg di cemento, dipende dal tipo e dalla classe di resistenza del cemento: maggiore sono il contenuto di clinker Portland e la finezza del cemento (cioè la classe di resistenza), più rapido è lo sviluppo di calore (Tabella 1).Il calore di idratazione provoca il riscaldamento del calcestruzzo. In condizioni adiabatiche, cioè in assenza di alcuna perdita di calore dal calcestruzzo, l’aumento di temperatura (?T_t)_ad, al tempo t, può essere così calcolato: q_t · c = m · r · (?T_t)_ad[1]dove q_t (in KJ/Kg) è il calore di idratazione unitario del cemento (Tabella 1), c è il dosaggio di cemento nel calcestruzzo (in Kg/m³), q_t · c (in KJ/m³ di calcestruzzo) è il calore sviluppato in 1 m³ al tempo t, m è la massa di 1 m³ di calcestruzzo (@ 2400 Kg/m³), r è il calore specifico del calcestruzzo [@ 1,1 KJ/(kg ·°C)]. In Fig. 5 è riportato l’incremento di temperatura (?T_t)_ad in funzione del tempo di idratazione (t) per un calcestruzzo con 300 Kg/m³ di cemento CEM II/A-L 42.5R in condizioni adiabatiche:(?T_t)_ad = q_t · 300/(2400 · 1.1) [2]Inserendo nella [2] I valore di q_t ai vari tempi (Tabella 1) si ricava la curva di Fig. 5.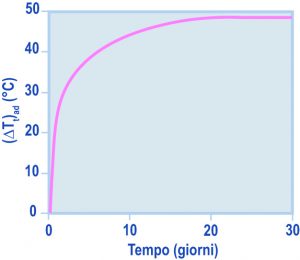Fig. 5 – Incremento di temperatura (?T_t) in funzione del tempo (t) calcestruzzo in condizioni adiabatiche: 300 kg/m³ di CEM II/A-L 42.5R 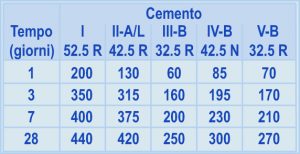Tabella 1 – Calore di idratazione (KJ/Kg) di alcuni cementi a vari tempi di idratazioneNel caso di un riscaldamento non adiabatico, come si verifica usualmente nelle strutture reali, l’andamento della temperatura sarà prima crescente (quando nei primi 2-3 giorni il calore d’idratazione si sviluppa ad alta velocità), e dopo decrescente (quando la dissipazione del calore dal calcestruzzo all’ambiente prevale sullo sviluppo del calore di idratazione che dopo 7 giorni procede più lentamente). Nella Fig. 6 è mostrato esemplificativamente ?T_t (in condizioni non adiabatiche) in funzione del tempo (t) in una zona della struttura termicamente più isolata (nucleo) ed in una zona corticale periferica dove il calore di idratazione è dissipato più rapidamente.A causa del diverso isolamento termico del calcestruzzo nella zona centrale (nucleo) ed in quella periferica, si instaura un gradiente termico (?T_t) tra la parte più calda e quella più fredda della struttura: ?T_t rappresenta il riscaldamento, cioè la variazione di temperatura in funzione del tempo (t) nello stesso punto della struttura, mentre ?T_t rappresenta il gradiente termico, cioè la differenza di temperatura, ad un determinato tempo (t), tra due diversi punti della struttura (nel caso specifico tra il nucleo, più caldo, e la periferia, più fredda).. Il massimo valore del gradiente termico (T)_max si raggiunge solitamente a 3 giorni e comunque raramente oltre 7 giorni (Fig. 6). Se il valore di (?T)_max supera 20°C esiste un rischio di fessurazione per le tensioni conseguenti alle differenti variazioni dimensionali. La fessurazione potrà apparire sulla superficie durante i primi 2-3 giorni (cioè nella fase di riscaldamento in Fig. 6) a causa delle tensioni di compressione nel nucleo più caldo (che vorrebbe dilatarsi) che provoca tensioni di trazione sulla superficie più fredda della struttura; in realtà questo tipo di rischio, che pure esiste, non è elevatissimo, perché il modulo elastico (E) è basso e, quindi, si instaurano basse tensioni a causa delle differenze termiche. Inoltre, si registra un rilassamento viscoso che mitiga le tensioni insorte tra nucleo e periferia.La fessurazione potrà verificarsi nel nucleo della struttura (quindi più insidiosamente perché non visibile) nella fase di raffreddamento di Fig. 6 per l’insorgere di tensioni di trazione nel nucleo che si raffredda più rapidamente della periferia. Poiché nel frattempo il calcestruzzo è diventato più rigido, le variazioni dimensionali di origine termica provocano una maggiore tensione. Inoltre, il rilassamento viscoso va diminuendo con l’aumento di rigidità del sistema, e quindi gioca un ruolo meno importante nel mitigare le tensioni.Mentre il calcolo di (?T_t)_ad in condizioni adiabatiche attraverso la [2] è relativamente semplice, il calcolo di (?T)_t è troppo complesso poiché dipende anche da fattori difficilmente prevedibili (condizioni eoliche e termiche nei giorni immediatamente dopo il getto) che influenzano la dispersione del calore, oltre che dalle dimensioni e dalla geometria delle strutture. Tuttavia, è possibile calcolare il valore di (?T)_max nella ipotesi estrema e conservativa di riscaldamento adiabatico nel nucleo e di dissipazione termica totale in periferia (temperatura sempre eguale a quella dell’ambiente): in queste condizioni il valore di (?Tt)_max coincide con quello di (?T_t)_ad; cioè la differenza di temperatura tra nucleo e periferia (Fig. 6) coincide con il riscaldamento adiabatico del nucleo (Fig. 5).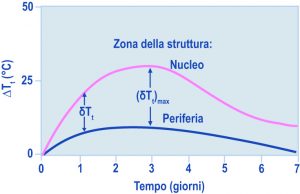Fig. 6 – Variazioni della temperatura (?T_t) in funzione del tempo (t) con formazione di gradienti termici (?T₃) in calcestruzzo non in condizioni adiabaticheAssumendo realisticamente che il (?T_t)_max è raggiunto solitamente a tre giorni si può porre:(?T₃)_max = (?T₃)_adAttraverso la [1] si ottiene(?T₃)_max = q₃ · c / m· r

Se si pone (?T₃)_max eguale a 20°C (massimo gradiente termico accettabile, oltre il quale esiste il rischio di fessurazione) si ottiene:

q₃ · c = 20 · m· r

Inserendo 2400 Kg/m² al posto di m, e 1,1 KJ/(Kg·c) al posto di r si ottiene:

q₃· c = 52800 KJ/m³

Scegliendo il tipo di cemento e conseguentemente il valore di q₃ dalla Tabella 1, si può calcolare il massimo dosaggio di cemento (c), attraverso la [6], per non superare il gradiente termico (?T₃)_max di 20°C. Per esempio il valore del dosaggio di cemento (c) diventa 167 Kg/m³ con il CEM II A-L 42.5R e 330 Kg/m³ se si sceglie il CEM III/B 42.5 con un minor calore di idratazione (q₃=315 e 160 KJ/kg rispettivamente).

Questo esempio mostra quanto si importante, per un getto massivo (platea di fondazione, diga, ecc.), la scelta di un cemento a basso calore di idratazione al fine di mantenere il rischio di fessurazione entro determinanti limiti pur impiegando un dosaggio di cemento abbastanza alto per ottenere un calcestruzzo sufficientemente coesivo e pompabile.

Umidità relativa al calcestruzzo

L’umidità relativa

L’umidità relativa (UR) rappresenta la percentuale della pressione del vapore acqueo (p) in un certo ambiente rispetto al valore massimo (p₀) della pressione del vapore quando è saturo (tensione di vapore):UR = (p/p₀)·100Poiché la tensione del vapore (p₀) aumenta con la temperatura (T), un certo valore di p corrisponde ad UR decrescente se aumenta T.Il valore di UR è 100% in un ambiente saturo di vapore. Se l’ambiente diviene insaturo (UR<100%) l’acqua libera che si trova nel calcestruzzo tende ad evaporare per saturare l’ambiente. Il processo prosegue finché teoricamente la pressione dell’ambiente non raggiunge il valore di p₀ (UR = 100%)*. In ambiente aperto, insaturo e ventilato, l’evaporazione prosegue continuamente senza mai poter saturare l’ambiente esterno; ciò provoca, ovviamente, un significativo essiccamento del calcestruzzo. Le conseguenze dell’essiccamento sono:. vulnerabilità delle armature metalliche alla corrosione (copriferro poroso);· minore resistenza meccanica nella struttura rispetto a quella dei provini;· rischio di fessurazione da ritiro plastico del calcestruzzo fresco;· rischio di fessurazione da ritiro igrometrico del calcestruzzo indurito.

L’influenza dell’UR sulla corrosione dei ferri di armatura

Il copriferro (cf) giuoca un ruolo di enorme importanza nella protezione delle armature metalliche dalla corrosione (Fig. 1): un copriferro poroso (in quanto esposto ad UR £ 95% e quindi essiccato) si lascia penetrare più facilmente dagli agenti ambientali che promuovono (CO₂, Cl^–) o alimentano (O₂, H₂O) la corrosione; d’altra parte, un copriferro di spessore (x) esiguo offre un cammino ridotto agli agenti aggressivi per arrivare ai ferri di armatura. Per esempio con un copriferro spesso 15 mm (Fig. 1), gli agenti aggressivi che penetrano il calcestruzzo secondo una legge del tipox = K ?t (calcestruzzo poroso)x = K’ ?t (calcestruzzo meno poroso) impiegheranno un tempo t₁ oppure t’₁ a seconda della porosità del copriferro (Fig. 1); d’altra parte raddoppiando lo spessore di copriferro da 15 a 30 mm (Fig. 1), i tempi di penetrazione degli agenti aggressivi diventano più lunghi:t’₁ > t₁(cf = 15 mm); t’₂> t₂(cf = 30 mm)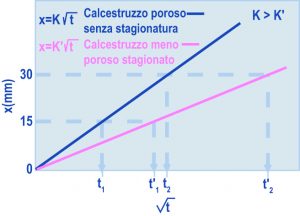

Fig. 1 – Influenza della porosità del calcestruzzo e dello spessore (x) di copriferro sul tempo (t) di penetrazione da parte degli agenti aggressivi

Pertanto, la protezione delle armature metalliche (in termini di tempo (t) impiegato dagli agenti aggressivi per raggiungere il ferro) è tanto maggiore quanto maggiore è x, e quanto minore è K. Questa, d’altra parte, dipende dalla porosità capillare V_p che a sua volta è funzione del rapporto acqua-cemento (a/c) adottato e del grado di idratazione (a) assicurato (si consulti l’articolo “Porosità e permeabilità del calcestruzzo”, sul sito www.encosrl.it è l’ABC del calcestruzzo).Riassumendo quanto sopra esposto:Pertanto, se si vuole assicurare una lunga protezione dei ferri di armatura (Ýt) occorre:· aumentare lo spessore di copriferro: Ýx· ridurre il rapporto acqua-cemento: ß a/c· aumentare il grado di idratazione: ÝaE’ sufficiente mancare in una delle tre summenzionate raccomandazioni per fallire nella protezione dei ferri di armatura e quindi nella durabilità della struttura.Le norme europee consentono di prescrivere, direttamente o indirettamente, valori di x, a/c, ed a tali da assicurare in pratica la durabilità delle strutture in c.a. e c.a.p.L’Eurocodice 2 fissa il valore minimo x in relazione al grado di aggressione ambientale (classe di esposizione), mentre la norma UNI-EN 206 stabilisce il valore massimo di a/c sempre in rapporto alla classe di esposizione (si consulti l’articolo “Durabilità del calcestruzzo armato”, sul sito www.encosrl.it è l’ABC del calcestruzzo.) Il valore di a è indirettamente prescritto (nella norma UNI-EN 206) attraverso alcune misure pratiche, atte a garantire una sufficiente idratazione del cemento per ridurre V_p secondo la [7] e quindi K secondo la [6]. Per raggiungere questo obiettivo occorre adottare in pratica una delle seguenti misure:– bagnare con acqua nebulizzata la superficie del calcestruzzo appena scasserata per almeno 3 giorni (preferibilmente 7 giorni);– mantenere umida la struttura appena scasserata mediante teli impermeabili o sacchi continuamente bagnati per almeno 3 giorni (preferibilmente 7 giorni);– rinviare la rimozione dei casseri al terzo giorno (preferibilmente al settimo) per mantenere umide le strutture;– proteggere la superficie applicando membrane anti-evaporanti in forma di agenti stagionanti (curing compound) nebulizzati sulla superficie della struttura scasserata (o subito dopo la presa nel caso dei pavimenti).Poiché tutte le procedure di stagionatura riportate hanno un costo (più alto nel rinviare la scasseratura, e più basso nell’applicare gli agenti stagionanti) difficilmente l’impresa ne adotterà una, per assicurare la durabilità delle strutture, se non verrà esplicitamente menzionata in una prescrizione di capitolato la specifica procedura con il riconoscimento del relativo costo.La mancata stagionatura umida delle superfici del calcestruzzo, lasciate al casuale tempo atmosferico dopo la scasseratura precoce (1 giorno), è tra le cause che concorrono alla formazione di un copriferro poroso (V_p elevato a causa di a basso) nonostante il basso rapporto a/c. Se il progettista ed il committente si rendessero conto dell’importanza di questo parametro (soprattutto nei lavori eseguiti in climi asciutti con UR < 95% e ventilati) si renderebbero conto della necessità di prescrivere e di controllare la procedura di stagionatura umida, riconoscendo all’impresa un costo a parte per questa operazione.

L’influenza dell’UR sulla resistenza meccanica

Si è già detto che la resistenza meccanica (R_c) dipende dal grado di idratazione a attraverso l’equazione di Powers (equazione [4] nell’articolo “Porosità e permeabilità del calcestruzzo” disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo ed anche Fig. 1 nell’articolo “Resistenza meccanica del calcestruzzo” disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo. Quest’aspetto del problema comporta un’ulteriore deviazione (oltre a quella provocata da una carente compattazione come è descritto nell’articolo “Lavorabilità del calcestruzzo fresco: influenza sul calcestruzzo in servizio”, disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo) tra resistenza meccanica del provino, che deve essere stagionato a umido (UR > 95%) per 28 giorni secondo la norma UNI 6127.311, e resistenza meccanica della struttura che difficilmente è altrettanto stagionata a umido. La Fig. 2 mostra l’influenza della UR sulla resistenza meccanica di un tipico calcestruzzo conservato sempre umido (UR=100%) oppure stagionato a umido soltanto per 1 o 7 giorni: si può vedere che, rimuovendo i casseri a un giorno e conservando il calcestruzzo in aria asciutta (UR=50%), la R_c si arresta dopo circa una settimana per l’evaporazione dell’acqua dal calcestruzzo e per il conseguente arresto nel valore di a; se, invece, la superficie del calcestruzzo è mantenuta umida per almeno 7 giorni (con una delle procedure già menzionate: stagionanti, acqua nebulizzata, ecc), la R_c a 28 giorni è appena di poco inferiore a quella del provino mantenuto umido fino a 28 giorni.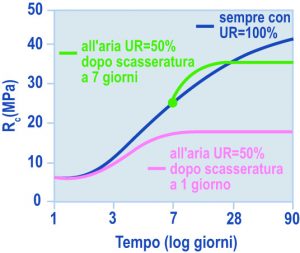

Fig. 2 – Influenza dell’UR sul decorso della resistenza meccanica

L’influenza dell’UR sul ritiro plastico

Il ritiro plastico è la contrazione che subisce il calcestruzzo quando si trova nella fase plastica del getto per l’evaporazione dell’acqua dalla superficie del calcestruzzo verso un ambiente insaturo di vapore (UR < 95%). Nelle strutture casserate, solitamente sformate a 1 giorno, il ritiro plastico non può ovviamente avvenire. Nei pavimenti, e nei calcestruzzi proiettati su muri o volte di gallerie, l’evaporazione dell’acqua può avvenire dalla superficie non casserata con una velocità tanto maggiore quanto più bassa è la UR dell’ambiente, quanto maggiore è la temperatura del calcestruzzo, quanto maggiore è la velocità del vento.Se le condizioni ambientali sono tali da far evaporare l’acqua ad una velocità superiore a 1 Kg/(m²·ora) esiste un rischio di fessurazione indotto dal ritiro plastico (?_p). Infatti, il ritiro e_p si tramuta in una tensione di trazione ?_t a causa del ritiro impedito** della parte epidermica coinvolta nell’essiccamento dalla superficie non casserata rispetto alla parte di calcestruzzo sub-corticale che rimane più protetta dall’essiccamento (si consulti ““F” come……Fessure, ma anche Fibre”, Enco Journal, N° 6). In realtà la tensione ?_tè modesta per il basso valore del modulo elastico (E_p) del calcestruzzo in fase plastica:?t = Ep ?pD’altra parte anche una tensione ?_t modesta è in grado di fessurare il calcestruzzo in superficie sotto forma di cavillature se la resistenza a trazione R_t è molto bassa come usualmente avviene in un calcestruzzo plastico (non ancora indurito) nelle prime ore dal getto:?_t> R_tPer evidenziare le fessure da ritiro plastico in un calcestruzzo appena indurito si può bagnare la superficie con acqua ed osservare la presenza di sottili cavillature che appaiono più scure per aver assorbito più acqua rispetto alla superficie di calcestruzzo che si asciuga più rapidamente ed appare più chiara.Per evitare le fessure da ritiro plastico in un pavimento sono possibili due strategie:1. evitare che in condizioni climatiche avverse (sole, vento, clima asciutto) la velocità di evaporazione dell’acqua superi il valore critico di 1 kg/(m²·ora) mediante applicazione di membrane anti-evaporanti o di acqua nebulizzata nella superficie appena finita: in sostanza occorre ridurre il ritiro plastico (?_p) ed invertire il segno di disuguaglianza della [9] diminuendo ?_t attraverso la riduzione di ?_p secondo la [8];2. rinforzare la matrice cementizia ed aumentare R_t mediante aggiunta di fibre polimeriche (poli-propileniche, poliacrilo-nitriliche, ecc.) in misura di 1-2 Kg/m³: in sostanza occorre invertire il segno di disuguaglianza della [9] aumentando R_t.La eliminazione delle microfessure da ritiro plastico è di fondamentale importanza per evitare, attraverso l’infiltrazione di acqua piovana, un degrado precoce delle pavimentazioni esterne soprattutto se armate.

L’influenza dell’UR sul ritiro igrometrico

Se un calcestruzzo è stagionato in ambiente con UR > 95%, o comunque protetto dal cassero o da altri mezzi che impediscono l’essiccamento, il materiale è dimensionalmente stabile. Se il calcestruzzo si trova sotto acqua tende leggermente a rigonfiare (swelling) per l’ingresso di acqua dall’ambiente all’interno del materiale. Se il calcestruzzo si trova in ambiente con UR < 95%, tende ad essiccarsi ed a contrarsi (Fig. 3), e l’effetto è noto come ritiro igrometrico.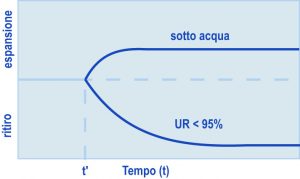

Fig. 3 – Effetto dell’umidità ambientale sulle variazioni dimensionali del calcestruzzo dopo scasseratura al tempo t’

Nel calcestruzzo sotto acqua, il rigonfiamento non rappresenta un pericolo di danno: perché la dilatazione (?_d) è modesta (o quasi nulla se il calcestruzzo era saturo prima dell’immersione in acqua) e perché la tensione di compressione (?_c), che si instaura in caso di vincolo alla dilatazione per la presenza dei ferri o di altri contrasti, non è in grado di superare la resistenza a compressione (R_c):R_c > ?_c = E ?_ddove E è il modulo elastico del calcestruzzo indurito ed e_d è la dilatazione del calcestruzzo che avverrebbe in assenza di vincoli per immersione sotto acqua.In un ambiente insaturo di vapore (UR < 95%), il calcestruzzo subisce un ritiro igrometrico (drying shrinkage, S) che dipende anche da molti altri fattori, quali la composizione del calcestruzzo, la percentuale dei ferri di armatura, la geometria della struttura, il tempo trascorso nell’ambiente insaturo. Per affrontare un problema così complesso è conveniente scindere il calcolo del ritiro igrometrico (S) in due stadi:-calcolo teorico del ritiro standard (S₀), cioè in ambiente e condizioni standard di laboratorio;-correzione del ritiro standard (S₀), mediante l’impiego di cinque coefficienti (f₁, f₂, f₃, f₄ ed f₅) per tramutare il ritiro standard in ritiro S in condizioni reali qualsiasi [11]S = S₀ S₁ S₂ S₃ S₄ S₅

Calcolo del ritiro standard di un provino

Il ritiro standard (S₀) è quello misurato nelle seguenti condizioni:· UR = 50%· tempo (t) = 6 mesi· geometria: provini di dimensione 10x10x50 cm con spessore fittizio*** (h) di 5 cm· armatura metallica (A): assente· inerte: calcareo con modulo elastico E_i di 40 GPaIn queste particolari condizioni il ritiro misurato a 6 mesi è funzione del rapporto a/c (tra 0,40 e 0,70) e del rapporto inerte/cemento i/c, tra 3 e 7, (Fig. 4). Il ritiro standard diminuisce al diminuire di a/c ed all’aumentare di i/c. La diminuzione di a/c comporta una pasta cementizia meno porosa e meno ricca in acqua capace di evaporare. D’altra parte, l’aumento di i/c comporta una maggiore presenza di inerte (a spese della pasta cementizia) che si oppone al ritiro per il suo maggior modulo elastico (Ei > E_p , dove Ei ed E_p sono i moduli elastici dell’inerte e della parte cementizia).Con una composizione del calcestruzzo di:c = 300 Kg/m³a = 180 Kg/m³i = 1900 Kg/m³i rapporti a/c ed i/c sono:a/c = 180/300 = 0.60i/c = 1900/300 = 6.33Dai valori di a/c (0.60) ed i/c (6.33) si calcola per S₀ un valore di 470 mm/m (Fig. 4).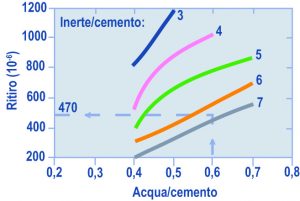

Fig. 4 – Ritiro standard a 6 mesi di provini 10x10x50 cm esposti in ambienti con UR=50% a 20°C

Calcolo del ritiro di una struttura reale

Per passare da S₀ (ritiro standard di un provino) ad S (ritiro della struttura) occorre precisare le condizioni reali nelle quali si intende valutare il ritiro igrometrico. Le Tabelle 1-5 presentano i valori dei coefficienti f₁, f₂, f₃, f₄ ed f₅ per i quali moltiplicare S₀ per passare ad S secondo l’equazione [11].Se, per esempio, si vuole calcolare il ritiro S nelle seguenti condizioni:t = 2 anniUR = 70%h = 20 cm (pilastro di sezione 40×40 cm)A = 1% (area occupata dalla sezione dei ferri rispetto alla sezione totale)inerte = basalto (E_i = 95 GPa)i coefficienti correttivi (f_i) diventano:f₁= 1,15 (Tabella 1)f₂= 0,70 (Tabella 2)f₃= 0,65 (Tabella 3)f₄= 0,85 (Tabella 4)f₅= 0,60 (Tabella 5)Con questi valori dei coefficienti corretti f_i, il ritiro S calcolato attraverso la [11] diventa:S = 470·1,15·0,70·0,65·0,85·0,60 = 125 mm/mCome si può vedere, i valori di f_i nelle Tabelle 1-5 possono far aumentare o mitigare il ritiro S rispetto a quello standard S₀. In particolare, fanno aumentare il ritiro: una UR minore; un tempo di esposizione più lungo in un ambiente insaturo di vapore; uno spessore fittizio più piccolo; una percentuale di armatura minore; ed un modulo elastico dell’inerte più basso. Ovviamente il ritiro è mitigato se i parametri sopra menzionati sono variati in senso opposto. Il ritiro è comunque nullo in strutture esposte in ambiente permanentemente saturo di vapore (UR > 95%) o immerse sotto acqua.Il ritiro può essere, entro certi limiti, ridotto a valori che non provocano gravi inconvenienti (S £ 500 mm/m); tuttavia, occorre sempre far presente che nelle strutture vincolate il ritiro non può manifestarsi liberamente, come con provini di laboratorio, e pertanto insorgono delle tensioni di trazione (?_t) che possono provocare la fessurazione delle strutture se la tensione a trazione ?_t supera la resistenza a trazione del calcestruzzo (si consulti l’articolo “Fessurazione del calcestruzzo: ingresso degli agenti aggressivi” , disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo. Per tramutare il ritiro S in tensione ?_t occorre tener conto sia del modulo elastico del calcestruzzo (E), ma anche del rilassamento, provocato dai fenomeni viscosi (ect) che mitiga la tensione di trazione (s_t):?_t= (S – ?_ct)Nell’articolo “Viscosità del calcestruzzo: deformazione viscosa o creep” (disponibile sul sito www.encosrl.it è l’ABC del calcestruzzo) saranno approfonditi gli aspetti legati ai fenomeni viscosi (creep) che attraverso la [12] fortunatamente spesso riducono ?_t al di sotto di R_t ed evitano quindi la fessurazione anche in presenza di ritiro vincolato.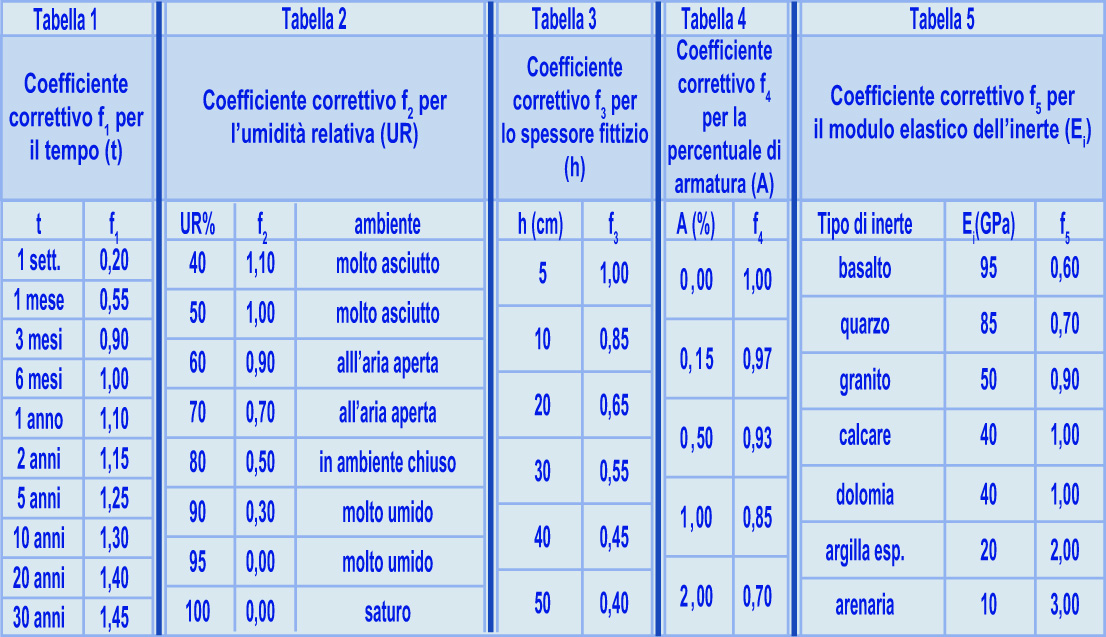NOTE* In teoria l’evaporazione dell’acqua è impedita solo in ambiente saturo di vapore (UR = 100%). Tuttavia, in pratica l’evaporazione dell’acqua dal calcestruzzo è nulla o trascurabile anche con UR = 95%. Ciò è dovuto al fatto che la tensione di vapore dell’acqua all’interno dei pori capillari (p’0) è leggermente inferiore rispetto a quella dell’acqua nell’ambiente (p₀). Per la stessa ragione, il vapore nei pori capillari condensa in corrispondenza di una tensione di vapore minore rispetto a quella dell’ambiente (condensazione capillare).**Il ritiro è impedito perché la parte epidermica, esposta all’evaporazione e quindi potenzialmente al ritiro, in realtà non può muoversi perché solidale con lo strato sub-corticale non esposto né all’evaporazione né al ritiro.***Lo spessore fittizio è il rapporto tra l’area della sezione ortogonale al ritiro ed il semi-perimetro esposto all’ambiente; nel caso dei provini per il ritiro standard, h = 10×10/(10 · 2) = 5 cm.

Viscosità del calcestruzzo: Deformazione viscosa o creep

Definizione del creep

La viscosità (o la deformazione viscosa o anche creep in inglese) rappresenta la variazione unitaria di lunghezza (?_c = ?l/l₀) quando il calcestruzzo indurito (dopo un certo tempo t₀ dal getto) è sottoposto all’azione di una sollecitazione di compressione (?‘_c) o di trazione (?‘_t) permanente per un determinato tempo t, di solito continuamente, più raramente variabile ciclicamente. Subito dopo l’applicazione di una generica sollecitazione s’, (di compressione o di trazione) al tempo t₀, il materiale si deforma immediatamente, e se la deformazione (?_e) non è molto grande, come solitamente avviene, essa si trova nel campo elastico, cioè obbedisce alla legge di Hooke (Fig. 1a) ed è facilmente calcolabile con l’equazione [1]:?_e = ?‘ /E [1]dove E è il modulo elastico.Se la sollecitazione s‘ viene conservata per un tempo t sufficientemente lungo, oltre alla deformazione elastica immediata (?_e), il materiale subisce un’ulteriore deformazione (?_c) che aumenta con il tempo (Fig. 1b) tendendo ad una valore limite asintotico (?_c?). La deformazione e_c è appunto il creep ed e_c? è il creep ultimo cui tende la deformazione viscosa dopo un tempo infinito (t = ?).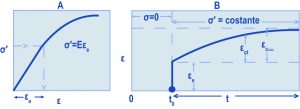Fig. 1 – A: Deformazione elastica istantanea ?_e misurata al tempo t₀ dal getto del calcestruzzo B: Deformazione viscosa ?_c successiva a quella elasticaSul ruolo importantissimo giocato dal creep nelle strutture in c.a. e c.a.p. si consiglia il lettore di leggere due articoli scritti da Adam Neville sui numeri di Maggio e Giugno di Concrete International (Creep of Concrete and Behavior of Structures Part I: Problems; Part II: Dealing with Problems). In particolare Neville sottolinea l’importanza di non fidarsi solo dei valori di creep riportati dai codici per il calcestruzzo, ma di tener conto della complessità del fenomeno sul quale agiscono ed interagiscono vari fattori. Alcuni di questi riguardano le condizioni di servizio (il carico che grava sulle strutture, la loro geometria ed il tempo di applicazione del carico), altri fattori riguardano le condizioni ambientali (l’umidità relativa), ed altri ancora le proprietà dello specifico calcestruzzo impiegato (dosaggio di cemento, rapporto a/c, modulo elastico e qualità dell’inerte) e non di un generico calcestruzzo come spesso impropriamente viene messo in conto dai progettisti quando si preoccupano delle conseguenze del creep.

Creep del calcestruzzo, creep puro e creep da essiccamento

Come si è sopra accennato il creep del calcestruzzo è funzione di un numero considerevole di parametri che includono:a) sollecitazione applicata s‘;b) modulo elastico (E) del calcestruzzo;c) umidità relativa (UR) dell’ambiente;d) tempo (t₀) di applicazione della sollecitazione contato a partire dal getto del calcestruzzo;e) composizione del calcestruzzo (a/c, c);f) geometria della struttura (spessore fittizio h);g) tempo t di mantenimento della sollecitazione contato a partire dal momento dell’applicazione della sollecitazione ?‘.Prima ancora di entrare nel dettaglio del creep in funzione dei vari parametri sopra riportati di carattere ambientare (UR), progettuale (?’, h, t), esecutivo (t₀) e composizionale (a/c, c, E), conviene esaminare l’interazione tra creep e ritiro che, nel caso di sollecitazioni a compressione (?’_c), sono dello stesso segno e si sommano. Nella Fig. 2 sono schematizzate tre possibili situazioni:a) una struttura in calcestruzzo in assenza di sollecitazioni (?‘_c=0), in ambiente insaturo di vapore, sottoposta ad un ritiro igrometrico (S) in assenza di vincoli a partire dal tempo di scasseratura (t₀), misurato a partire dal momento del getto (t=0);b) una struttura in calcestruzzo, in ambiente saturo di vapore (UR = 95-100%) e quindi priva di ritiro, sottoposta, al tempo t₀, ad una sollecitazione ?’_c che provoca una deformazione elastica ?_e cui si somma la successiva deformazione ?_c da creep (deformazione totale ?_T= ?_e+?_c): il valore di ?_c misurato in queste condizioni, cioè in assenza di ritiro, prende il nome di creep puro o creep fondamentale;c) una struttura in calcestruzzo esposta al tempo t₀ in ambiente insaturo di vapore che provoca un ritiro S, e simultaneamente sottoposta alla sollecitazione (?‘_c): in queste condizioni la deformazione totale (?_T) risulta maggiore della somma dei singoli contributi alla deformazione (?_e, ?_c, S):?_T > ?_e + ?_c + S [2]Fig. 2: a – Contrazione da ritiro (S) in ambiente insaturo di vapore (UR<95%) ed in assenza di sollecitazione; b – Contrazione elastica iniziale (?_e) seguita da quella da creep puro (?_c) in presenza di una sollecitazione a compressione costante (?‘_c) in ambiente saturo di vapore;c – Deformazione totale (?_T) dovuta alla deformazione elastica iniziale (?_e), più la deformazione da creep puro (?_c), più la deformazione da ritiro (S), più la deformazione da creep da essiccamento (?_d).La differenza tra la deformazione totale ?_T misurata nelle condizioni della Fig. 2c, e la somma dei singoli contributi deformazionali prende il nome di creep da essiccamento (drying creep) e viene indicato con il simbolo ?_d (area punteggiata in Fig. 2c). La deformazione totale diventa pertanto:?_T = ?_e + ?_c + S + ?_d[3]Ciò significa che, sotto la sollecitazione di compressione ?‘_c in ambiente insaturo di vapore, l’evaporazione dell’acqua è maggiore di quella che si registra in assenza di ?‘_c e che determina il ritiro S: la maggiore evaporazione dell’acqua – una sorta di “effetto spremitura” del calcestruzzo a compressione – comporta una maggiore deformazione addizionale (?_d) che si somma agli altri contributi deformazionali. In particolare il contributo del creep totale (?_cT) è dato dalla somma del creep puro ?_c e dal creep da essiccamento (?_d):?_cT = ?_c + ?_d[4]La [4] pertanto può anche essere scritta in forma di?_T = ?_e+ S + ?_cT [5]Per il calcolo della deformazione totale ?_T in una struttura esposta al ritiro (S) ed al creep (?_cT) determinato dalla sollecitazione (?‘_c) applicata al tempo t₀, la [5], tenendo conto della [1], diventa:?_T = (?’_c/Et0) + S + ?_cT [6]dove E_t0 è il modulo elastico del calcestruzzo al tempo (t₀) quando si applica la sollecitazione ?‘_c. Il calcolo di S è trattato nell’articolo “Umidità Relativa” presente su www.encosrl.it. Di seguito è descritto il calcolo del creep totale (?_cT), da sommare al contributo elastico (?‘_c/E_t0) ed al ritiro (S), per determinare la deformazione totale (?_T) igro-elastico-viscosa in qualsiasi condizione.

Calcolo del Creep

Se si applica una sollecitazione a compressione ?‘_c al tempo t₀ il creep totale ?_cT può essere espresso in funzione della sollecitazione (?‘_c):?_{cT =}(?‘_c/E₂₈) * a [7]dove ?‘_c/E₂₈ è la deformazione elastica nominale*, cioè quella deformazione elastica che si otterrebbe se ?‘_c fosse applicata a 28 giorni anziché al generico tempo t₀, e dove a è un coefficiente moltiplicativo funzione di cinque parametri g_i :a = g_{1 *}g_{2 *} g_{3 *} g₄ * g₅[8]Il creep totale (?_cT), inserendo la [8] nella [9], diventa:?_{cT =}(?‘_c/E₂₈) * g_{1 *}g_{2 *} g_{3 *} g₄ * g₅ [9]dove- g₁ è funzione dell’umidità relativa UR (Fig. 3);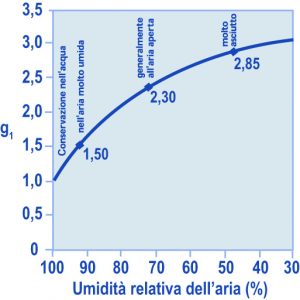Fig. 3- Fattore g₁ (umidità relativa) in funzione dell’umidità relativa (“Scienza e tecnologia del calcestruzzo” di M. Collepardi, III Ed, Hoepli, 1991, Milano).– g₂ è funzione dell’età del calcestruzzo (t₀) quando si applica s‘_c e della classe di resistenza del cemento (Fig. 4);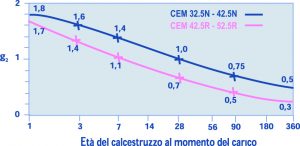Fig. 4 – Fattore g₂ (stagionatura del calcestruzzo) in funzione del tempo (in giorni) prima dell’applicazione del carico (“Scienza e tecnologia del calcestruzzo” di M. Collepardi, III Ed, Hoepli, 1991, Milano).– g₃è funzione della composizione del calcestruzzo ed in particolare di a/c e c (Fig. 5);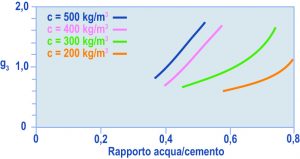Fig. 5 – Fattore g₃ (composizione del calcestruzzo) in funzione del rapporto acqua/cemento. I numeri sulle curve indicano i dosaggi di cemento (“Scienza e tecnologia del calcestruzzo” di M. Collepardi, III Ed, Hoepli, 1991, Milano).– g₄ è funzione della geometria della struttura attraverso lo spessore fittizio h (Fig. 6);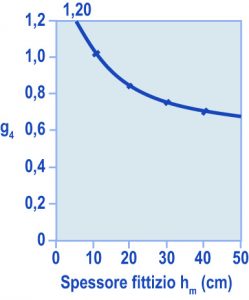Fig. 6 – Fattore g₄ (spessore della struttura) in funzione dello spessore fittizio (“Scienza e tecnologia del calcestruzzo” di M. Collepardi, III Ed, Hoepli, 1991, Milano).– g₅ è funzione del tempo (t) di applicazione del carico (Fig. 7).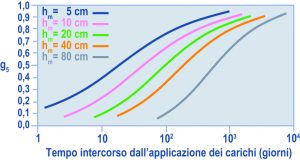Fig. 7 – Fattore g₅ (tempo di sollecitazione) in funzione della durata della sollecitazione (“Scienza e tecnologia del calcestruzzo” di M. Collepardi, III Ed, Hoepli, 1991, Milano), hm è lo spessore fittizio. L’analisi dei fattori correlati con i coefficienti g_i (tutti adimensionali) può essere così riassunta:- al diminuire dell’UR il coefficiente g₁ aumenta significativamente e raggiunge valore di 2-3 per una UR del 50-75% (Fig. 4); ciò comporta un eguale aumento del creep a parità di tutte le altre condizioni; val la pena di segnalare che in ambienti saturi (UR = 100%) o comunque quando l’evaporazione è impedita, g₁ è eguale ad 1 e equivale a dire che il creep di essiccamento (?_d), ma anche il ritiro (S) nella Fig. 2c, sono nulli, cioè il creep totale ?_cT coincide con il creep puro (?_c) della Fig. 2b;-g₂ diminuisce se si aumenta l’età (t₀) di applicazione del carico e se si impiega un cemento di maggior classe di resistenza (Fig. 4): in sostanza g₂ diminuisce quanto più il calcestruzzo risulta meccanicamente resistente al momento dell’applicazione del carico;- g₃ (Fig. 5) diminuisce al diminuire del rapporto a/c (cioè con una matrice cementizia più resistente meccanicamente) ed al diminuire del dosaggio di cemento (c), cioè con la riduzione del volume di matrice cementizia più deformabile della componente lapidea (almeno con aggregati naturali usuali): in altre parole l’impiego di superfluidificanti per ridurre a/c o per ridurre c sono favorevoli alla riduzione di g₃ e quindi del creep; analogo effetto può essere conseguito con l’adozione di un maggiore diametro massimo per l’inerte;- g₄ diminuisce con la “massività” della struttura, cioè all’aumentare dello spessore fittizio h definito come rapporto tra sezione (A) della struttura ortogonale alla direzione di applicazione del carico e semiperimetro (S_p) esposto all’ambiente: in sostanza strutture più massive (cioè con un h più elevato) si deformano meno;- g₅ aumenta con il trascorrere del tempo t dopo l’applicazione del carico e cresce più rapidamente con le strutture “snelle” (h piccolo) che non con le strutture “massive” (h grosso); per un tempo infinito (g₅ = 1), il creep ?_cT così calcolato corrisponde al creep ultimo (?_c? in Fig. 1).

Applicazione numerica

Un esempio numerico chiarirà il modo per calcolare il creep totale ?_cT con la [9] da aggiungere alla deformazione elastica ?‘_c/E_t0 ed al ritiro S (calcolati separatamente) per determinare la deformazione totale ?_T con la [6].Un pilastro (20×20 cm) in calcestruzzo è sollecitato a compressione con una massa di 10 Ton dopo 7 giorni dal getto. Il calcestruzzo è stato confezionato con 350 kg/m³ di cemento CEM 32.5 e con a/c = 0,50 (R_ck = 40 MPa).Calcolare il creep totale (?_cT) dopo 3 mesi (@100 gg) e dopo 3 anni (@1000gg) dall’applicazione del carico ipotizzando una UR media del 70%; calcolare, inoltre, il creep totale ultimo, cioè a tempo infinito:?‘_c= (10 Ton / 20-20 cm²) = (10000 Kg / 400 cm²) = 25 kg/cm² = 2,5 MPaE₂₈ = 5700 ?40 = 36000 MPaUR = 70% —> g₁ = 2,3 (Fig. 4)CEM 32,5 + 7 giorni dal getto —> g₂ = 1,4 (Fig.5)c = 350 kg/m³ + a/c = 0,50 —> g₃= 1,0 (Fig.6)20-20cm —> hm = 20-20/2-20 = 10 cm —> g₄= 1,0 (Fig.7)tempo di applicazione del carico = 100 gg + hm = 10 cm —> g₅= 0,65 (Fig.8) tempo di applicazione del carico = 1000 gg + hm = 10 cm —> g₅= 0,90 (Fig.8) Il valore ?_cT a 100 giorni è:?_cT= 2,5 / 37000 * 2,3 * 1,4 * 1,0 * 1,0 * 0,65 = 141 * 10ˆ-6 = 141 ?m/mIl valore ?_cT a 1000 giorni è:?_cT= 2,5 / 37000 * 2,3 * 1,4 * 1,0 * 1,0 * 0,90 = 195 * 10ˆ-6 = 195 ?m/mD’altra parte inserendo il valore di g₅=1 si calcola il creep ultimo:?_c?= 220 * 10ˆ-6 = 220 ?m/mQuesta deformazione unitaria, nel caso di un pilastro alto 10 m corrisponde ad un accorciamento assoluto (?l) a tempo infinito di 2,2 mm:?l = ?_{c? *}10= 220 * 10 = 2200 ?m = 2,2 mm Nota* ?’_c/E₂₈ non è la vera deformazione elastica se la ?‘_c è applicata, come solitamente avviene, ad un tempo t₀ diverso da 28 giorni; la vera deformazione elastica, che appare nella Fig.2 e nell’equazione [6], è ?‘_c/E_t0 ed è maggiore di ?‘_c/E₂₈ se t₀ < 28 giorni poiché E_t0 < E₂₈. Il calcolo di s‘_c/E₂₈ richiede la conoscenza della sollecitazione ?‘_c (applicata al generico tempo t₀) e del modulo elastico E₂₈ calcolabile dalla R_ck con l’equazione [12] dell’articolo “Resistenza meccanica del calcestruzzo” presente sul sito www.encosrl.it è l’ABC del calcestruzzo. I valori di ?‘_c e di R_ck sono desumibili dal progetto della struttura.

A B C Calcestruzzo

LAVORABILITÀ, ACQUA, INERTE, ADDITIVI

RESISTENZA CARATTERISTICA, CEMENTO E RAPPORTO A/C

DURABILITÀ, RAPPORTO A/C ED ARIA INGLOBATA

COMBINAZIONE DEGLI INERTI DISPONIBILI

PER CONCLUDERE

FOTOGRAFIA

TERMOGRAFIA

ENDOSCOPIA

MAGNETOMETRIA

GAMMAGRAFIA

AUSCULTAZIONE SONICA

RILEVAMENTO DEGLI ULTRASUONI

SCLEROMETRIA

L’APPROCCIO RIDUZIONISTICO

L’APPROCCIO OLISTICO

IL RUOLO DELL’ACQUA

Quanti tipi di pori nel calcestruzzo

Porosità capillare e resistenza meccanica

Porosità capillare e permeabilità

Porosità capillare e durabilità

Costanza di qualità del calcestruzzo

L’umidità dell’inerte

Influenza dell’umidità dell’inerte sulle prestazioni del calcestruzzo

Modifica delle pesate degli ingredienti rispetto al mix-design

Modifica delle pesate degli ingredienti rispetto al mix-design

Quale resistenza meccanica

Resistenza Meccanica a compressione: il ruolo di a/c e a

Resistenza meccanica a compressione del calcestruzzo

Resistenza caratteristica Rck

Resistenza meccanica a flessione ed a trazione

Correlazione tra Rc ed Rf o Rt

Correlazione tra Rc ed E

Gli additivi

L’avvento dei superfluidificanti

Le “tre facce di una stessa medaglia”

Aggiunta del superfluidificante a pari composizione del calcestruzzo

Aggiunta del superfluidificante a pari lavorabilità con riduzione di acqua e di a/c

Aggiunta del superfluidificante a pari lavorabilità ed a/c con riduzione di acqua e cemento

Conclusioni

Influenza della temperatura sulle prestazioni meccaniche

Influenza della temperatura ambientale sul getto in cantiere

Trattamento termico del calcestruzzo in prefabbricazione

Calore di idratazione, gradienti termici e rischi di fessurazione

L’umidità relativa

L’influenza dell’UR sulla corrosione dei ferri di armatura

L’influenza dell’UR sulla resistenza meccanica

L’influenza dell’UR sul ritiro plastico

L’influenza dell’UR sul ritiro igrometrico

Calcolo del ritiro standard di un provino

Calcolo del ritiro di una struttura reale

Definizione del creep

Creep del calcestruzzo, creep puro e creep da essiccamento

Calcolo del Creep

Applicazione numerica

Iscriviti alla newsletter

Articoli recenti

**Resistenza Meccanica a compressione: il ruolo di a/c e** a

Resistenza caratteristica R_ck

Correlazione tra R_c ed R_f o R_t

Correlazione tra R_c ed E